engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Analysis of the Numerical Methods for a Fractional Dirac Equation
1Department of Applied Mathematics for Information Technology, E.T.S.I. Telecommunication, Polytechnic University of Madrid, Spain
2State Key Laboratory of Scientific and Engineering Computing, Chinese Academy of Sciences, Beijing, China
| (43) |
In order to build our numerical scheme, we start using the ideas presented in [3] for a system that depends on a single variable, we will then extend the ideas to the fractional equation. We start considering a fractional equation of the form:
where
| (45) |
the equation is equivalent to
For this equation we have build two first order schemes. Combining both, we can build a second order scheme:
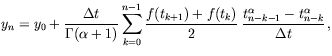 |
(47) |
with local truncation error:
| (48) |
and
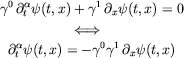 |
(49) |
and from here
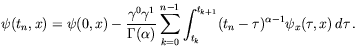 |
(50) |
Denoting the spatial index by subscripts and the temporal one by superscripts, we have the numerical scheme
The local truncation error can be written as
| (52) |
for some
We show that, under reasonable boundary and initial conditions, the errors at each time-step are bounded by an expression that goes to zero as the mesh sizes go to zero, keeping both a finite fixed time and a spatial length. The scheme is thus convergent.
- 1
- A.A. Kilbas, T. Pierantozzi, J.J. Trujillo and L. Vázquez. "On the Solution of Fractional Evolution Equations", Journal of Physics A, 37, 3271-3283 (2004). doi:10.1088/0305-4470/37/9/015
- 2
- T. Pierantozzi and L. Vázquez, "An interpolation between the wave and diffusion equations through the fractional evolution equations Dirac like", Journal of Mathematical Physics, 46, 113512-113523 (2005). doi:10.1063/1.2121167
- 3
- G. Turchetti, D. Usero and L. Vázquez, "Hamiltonian systems with fractional time derivative", Tamsui Oxford Journal of Mathematical Sciences, Vol 18 (1), 31-44 (2002).
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)