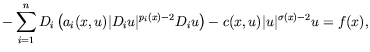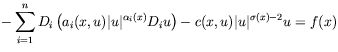Keywords: elliptic equation, nonstandard growth conditions, variable nonlinearity, localization, anisotropy.

We study the Dirichlet problem for the elliptic equations with variable anisotropic nonlinearity

The boundary is Lipschitz-continuous. The coefficients , c and the exponents of nonlinearity , , are prescribed functions of their arguments. Equations of the type (37), (38) emerge from the mathematical modelling of various physical phenomena, e.g., the processes of image restoration, flows of electro-rheological fluids, thermistor problem, filtration through inhomogeneous media.

For the existence of solutions [1,2], we prove that under suitable restrictions on the coefficients and the nonlinearity exponents the Dirichet problem for equations (37) and (38) admit an a.e. bounded weak solutions which belong to the anisotropic analogs of the generalized Lebesgue-Orlicz spaces. The solution of equation (37) is constructed as the limit of a sequence of Galerkin's approximations. We claim that , , , and that the exponents are continuous with a logarithmic module of continuity.

The existence of an a.e. bounded weak solution of equation (38) is proved by means of the Schauder fixed point principle. It is requested that and either in and , or and .

For the uniqueness of solutions [2,3], it is shown that a.e. bounded (small) solution of equation (37) is unique if and either , and is Lipschitz-continuous with respect to s, or if , and .

For equation (38), the uniqueness of bounded solutions is proved for the assumptions that , , , .

For localization of solutions caused by the diffusion-absorption balance [2], a localization (or vanishing on a set of nonzero measure) is an intrinsic property of solutions to nonlinear elliptic equations. It is known that for the solutions of equations of the type (37), (38) with constant (but possibly anisotropic) nonlinearity such an effect appears due to a suitable balance between the diffusion and absorption terms of the equation. We show that the same is true for equations with variable exponents of nonlinearity. The proof relies on the method of local energy estimates.

For directional localization caused by anisotropic diffusion [1,3], it is known that for the solutions of nonlinear equations of the type diffusion-absorption the following alternative holds: if u is a nonnegative weak solution of the exterior Dirichlet problem for the equation with constant exponents p and , then

It turns out to be that this alternative is no longer true if the diffusion operator is anisotropic. In this case the support of the solution may be compact even in the absence of the absorption part. Similar assertions hold for the solutions of equation (37). The property of directional localization allows one to solve problems posed on unbounded domains without additional conditions at infinity. Sufficient conditions of solvability read as restrictions on the asymptotic shape of the domain as . For example, in the case it is sufficient to claim that is contained in a cone of aperture less than .

Most of the results extend to solutions of equations of the type (37), (38) with the first-order terms (convection) and to systems of equations of similar structure [2,3].

1

S. Antontsev and S. Shmarev, On localization of solutions of elliptic equations with nonhomogeneous anisotropic degeneracy, Siberian Mathematical Journal, 46 (2005), doi:10.1007/s11202-005-0076-0pp. 765-782.

2

S. Antontsev and S. Shmarev, Elliptic equations and systems with nonstandard growth conditions: existence, uniqueness and localization properties of solutions, To appear in Nonlinear Analysis Serie A: Theory & Methods, (2006). doi:10.1016/j.na.2005.09.035

3

S. Antontsev and S. Shmarev, Handbook of Differential Equations, Stationary Partial Differential Equations., vol. 3, Elsevier, To appear, p. 109 pp.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)