Keywords: fractional calculus, fractional-order systems, fractional-order differential equations, complex-order derivatives, complex-order systems, complex-order differential equations.

The idea of an integer-order differintegral operator has previously been extended to a differintegral operator of non-integer, but real, order. Further generalizations have been made to the complex-order operator. Hartley, et al. [1] showed that when a complex-order operator is paired with its conjugate-order operator, real time-responses are created. Further, as long as the coefficients of the operators are complex-conjugates, a real time-response results [1]. Systems with complex-order differintegrals can arise from a variety of situations. They appear to arise naturally with the Cauchy-Euler differential equation. The CRONE controller [2] makes use of conjugated-order differintegrals in a limited manner. Such a system can result from system identification. A system with complex-order can also be artificially constructed and implemented using FPGA techniques.

The system whose transfer function is , has an impulse response that is given by the F-function as given by Hartley and Lorenzo [3]. The derivation of the F-function is valid for complex values of q and k. The impulse response, , is in general complex. The system whose transfer function is , has an impulse response that is the sum of complex conjugate F-functions, that is, . This is a real-valued function for any complex values of k, p and q. This function is also written as

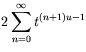This function represents the impulse response of the differential equation

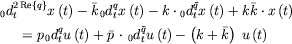The poles of the transfer function, are located at , where and . The paper demonstrates that there are a finite number of poles on the primary Riemann sheet for systems whose order is not purely imaginary. The bounds on for a stable system are found to be the intersection of disks with center in the fourth quadrant whose boundary contains the origin in the u-v plane. The paper also shows that a stable complex-order system has at most four poles on the primary Riemann sheet.

The Bode magnitude plot has expected characteristics. For frequencies much less than a critical point, the magnitude is constant. For frequencies much greater than a critical point, the magnitude response has a slope of , with some ripple which is dependent on the value of v. The magnitude response for frequencies relatively close to the critical point depends on k, p and q in a nontrivial manner.

Several examples serve to verify the analytical results. One example shows that these systems can display the interesting feature of dual fractional-order resonances. Specifically, consider . This system has primary Riemann-sheet poles at and . The step response exhibits two frequencies that correspond to these two imaginary frequencies. The frequency response contains two resonances, one at each of these frequencies. The analysis presented in this paper serves as a foundation for the study of complex-order systems involving more conjugate-order pairs.

1

T.T. Hartley, C.F. Lorenzo, and J.L. Adams, "Conjugated-Order Differintegrals", Proc. of 2005 ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Long Beach, CA, USA, September 24-28, 2005. doi:10.1115/DETC2005-84951

2

A. Oustaloup, J. Sabatier, and P. Lanusse, "From fractal robustness to CRONE control", Fractional Calculus and Applied Analysis, vol. 2, no. 1, 1-30, 1999.

3

T.T. Hartley, C.F. Lorenzo, "Dynamics and Control of Initialized Fractional-Order Systems", Nonlinear Dynamics vol 29 (1-4), 201-233, 2002. doi:10.1023/A:1016534921583

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)