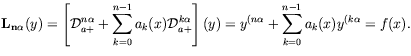Keywords: fractional differential equations, linear fractional differential equations, Caputo fractional derivative, Riemann-Liouville fractional derivative.

Many great mathematicians have been interested in fractional operators and its applications during the last 170 years. It is known that the classical calculus provides a powerful tool for explaining and modelling many important dynamic processes in most applied sciences. But experiments and reality teach us that there are many complex systems in nature and society with anomalous dynamics, from the spread of contaminants in underground water or relaxation in viscoelastic materials like polymers, to the transmission of signals through strong magnetic fields such as those found within confined plasma, and many more.

In most of the above-mentioned cases, this kind of anomalous process has a complex macroscopic behaviour, the dynamics of which cannot be characterised by classical derivative models. Nevertheless, a heuristic solution to the corresponding models of some of those processes can be frequently obtained using tools from statistical physics. Such tools have been used extensively during last forty years. But the connection between these statistical models and certain fractional differential equations involving the fractional integral and derivative operators (Riemann-Liouville, Caputo, Liouville or Weyl, Riesz, etc.) has only been formally established during the last fifteen years and more intensively during the last five years.

What are the useful properties of these fractional calculus operators which help in the modelling of so many anomalous processes? From the point of view of the authors and from known experimental results, most of the processes associated with complex systems have non-local dynamics involving long-memory in time, and the fractional integral and fractional derivative operators do have some of those characteristics. Perhaps this is one of the reasons why these fractional calculus operators lose the above-mentioned useful properties of the ordinary derivative D.

We may conclude from the foregoing presentation that it is important to work out a rigourous theory of fractional differential equations analogous to that for ordinary differential equations. In fact, there are many similar and new open questions in this subject, the answers to which can help in the development of the applied sciences. Let us mention here, as an illustrative historical example, that the delta function, introduced by Dirac at the end of nineteenth century, has been formally used by physicists in many of their ordinary derivative models for a long time, yet their investigations became rigourous only about fifty years later, when Laurent Schwartz presented his distribution theory in 1944.

This paper presents the basic general theory for sequential linear fractional differential equations, involving the Caputo fractional operators, ( )

where are continuous real functions defined in and

We then introduce the Mittag-Leffler type function , which we will call Caputo -exponential, and certain fractional Green functions. This function allows us to introduce a new direct method to obtain the general solution of the homogeneous and non-homogeneous case with constant coefficients of (35). Finally, such theory it is applied to obtain the solution of some boundary value problems.

We must point out that the Laplace or Fourier Transform can not solve many problem connected with the linear fractional differential equations, for example boundary value problems.

The theory presented in this paper opens the possibility for the development of a generalised theory analogous to that of Sturm-Liouville for linear fractional differential equations of second order involving the Caputo derivative. So we, also, open the possibility for applying the separation of variables method to solve boundary value problems associated with partial fractional models, such as fractional diffusion or wave models involving spatial-fractional derivatives, as an alternative to the integral transform methods. On the other hand, it is well known that the so called fractional Fourier transform is a new tool developed during the last decade which has many applications in signal and optical theory. The generalised trigonometric functions introduced in this paper give us the opportunity to develop a generalised Fourier analysis theory involving fractional Fourier series and a new and more natural concept of the fractional Fourier transform, analogous to the corresponding one in the ordinary case.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)