Keywords: lateral-torsional buckling, web-tapered beams, buckling analysis, one-dimensional variational formulation, pre-buckling deflections, I-section cantilevers, Rayleigh-Ritz method, shell finite element analysis.

In recent years, the use of thin-walled tapered structural members (i.e., non prismatic members with a continuous cross-section variation) has gained an increasing popularity in the steel construction industry, mainly because of their efficiency and aesthetics. Open-section flexural members, either prismatic or tapered, are prone to lateral-torsional buckling (LTB) and, therefore, it would be most convenient, for the sake of uniformity and ease-of-use, to have design methodologies that are valid for both prismatic and tapered beams. In order to achieve this goal, the most "natural" approach consists of extending the prismatic beam rules and procedures already available in the current steel design codes, making them also valid for the design of tapered beams. Indeed, this was precisely the approach followed in the most recent "preliminary version" of the upcoming EN version of Eurocode 3. Hence, the need arises to develop efficient and accurate methods to evaluate the elastic critical load parameter (i.e., the load parameter associated with the first bifurcation point) of a given tapered beam, a necessary step towards the determination of its slenderness.

Very recently, the first two authors derived a one-dimensional (1D) formulation to analyse the elastic LTB behaviour of singly symmetric tapered thin-walled open beams, which (i) is able to account for the influence of the pre-buckling deflections and (ii) clearly shows that, in general, the behaviours of prismatic and tapered beams are qualitatively different. This 1D formulation is based on a number of a priori assumptions (which, in fact, are an extension of the classical Vlassov's hypotheses of prismatic thin-walled beam theory) and was only validated through the comparison with LTB results reported by other researchers, also relying on more or less similar a priori assumptions. Therefore, it becomes necessary to further (i) validate these assumptions and (ii) assess the merits of the 1D model that they bring about. This is precisely the central objective of this work, in which a comparison is made between (i) the global performance of the above 1D formulation (numerically implemented by means of the Rayleigh-Ritz method) and (ii) the results yielded by shell finite element analyses (FEA). The latter are performed in the code ABAQUS and their results are deemed "exact". The FEA are also used to check the validity of one of the kinematical assumptions underlying the 1D model (the one stating that the cross-sections remain undeformed in their planes). This comparative study concerns I-section cantilevers (i) with equal/unequal uniform flanges and uniform/linearly tapered webs, which (ii) are acted by point loads applied at various locations of the free end section.

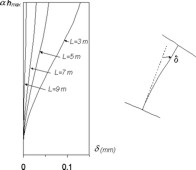
The paper begins with a brief review of the 1D formulation. Next, the most relevant aspects involved in the LTB shell FEA of (prismatic and tapered) beams are addressed, including (i) the adequate discretisation of the beams, (ii) the numerical procedure used to solve the eigenvalue problem arising in the linear stability analysis (pre-buckling deflections neglected) and (iii) the approach devised to account for the pre-buckling deflections. Finally, the results of the comparative study are presented and discussed. They consist of (i) 1D and FEA-based linear (i.e., obtained by neglecting the pre-buckling deflections) and non-linear critical loads, and (ii) the associated critical buckling modes - Figure 1(a). Also shown is the free end section web distortion appearing in the FEA-based critical modes, which makes it possible to assess how much the web "true" deformed shape deviates from the one generated by an in-plane rigid body rotation - Figure 1(b).

On the basis of this study, it is possible to say that, as long as the cantilevers are not too short, the one-dimensional formulation leads to reasonably accurate estimates of the critical loads and buckling mode shapes, regardless of whether the pre-buckling deflections are taken into account or not. Moreover, the accuracy of these estimates gradually increases with the cantilever length, a trend that reflects the decreasing relevance of the web distortion taking place near the free end section. To a certain extent, this fact validates one of the a priori assumptions incorporated in the one-dimensional model. As for the considerable differences between the 1D and shell finite element models recorded for the shorter cantilevers, they are mainly due either to (i) significant web distortion or (ii) a localised web buckling phenomenon, which occur in the neighbourhood of the load point of application. Obviously, none of these local effects can be captured by the 1D formulation.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)