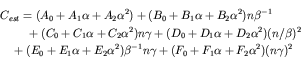Keywords: linearly tapered column, taper parameter, sectional property parameter, elastic critical load, natural frequency of lateral vibration, regression analysis.

In the case of single prismatic members, the axial thrust, and the reduced lateral vibration frequency, , due to , are generally related by the following equation:

where and denote the elastic critical load and the fundamental natural frequency of lateral vibration, respectively. Experimental tests on rigid rectangular frames with prismatic columns show that the relationship given by Equation (<72) is also applicable with minimal error [1,2].

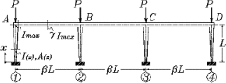
For the rectangular frames with nonprismatic columns, however, the two (eigenvalues elastic critical load and fundamental natural frequency) are hard to determine and the above relationship is in question. This paper aims to examine whether Equation (72) is also applicable to the rectangular frame shown in Figure 1. The following shows the parameters and other factors considered in the eigenvalues analysis of the frame by the finite element method.

The shape functions for the linear element having two degrees of freedom at each node is utilized in the formulation of element matrices [3,4]. When the element matrices are assembled for the whole structure, the external force, , and the external displacement, are related by the following equation:

where , and denote the assembled matrices for the whole structure.

Due to the large size of assembled matrices, the eigenvalues are determined by a computer-aided iteration method. The determinations of the first mode eigenvalues by the iteration method easy when Equation (73) is transformed into the following form:

where is the unit or identity matrix. Two eigenvalues are determined by subdividing the tapered column into 20 equal elements and the prismatic beam into 2 equal elements.

To generalize the changes of eigenvalues obtained by the finite element method, the following form second order algebraic equations is proposed:

The constants are determined by the regression technique [5]. To obtain the lateral frequencies of the structure under the variable thrust, , Equation (73) is transformed into the following form:

where is the load ratio . By changing from 0.0 to 1.0 with subinterval, =0.2, the corresponding frequencies are calculated by Equation (75). The computed results show that Equation (72) is also applicable to the rectangular frames with tapered columns.

1

H. Lurie, "Lateral Vibrations as Related to Structural Stability", Jour. of Applied Mechanics Div., ASME, V.10, V.12, September, pp.195-203, 1952.

2

Z.P. Bazant, L. Cedolin, "Stability of Structures", Oxford University Press, 1991.

3

A. Chajes, "Principles of Structural Stability Theory", Prentice-Hall. Inc, 1974.

4

M. Paz, "Structural Dynamics, Van Nostrand Reinhold Co., Inc, pp.402-407, 1985.

5

M.R. Spiegel, "Probability and Statistics", McGraw-Hill, Inc, pp.258-264, 1975.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)