
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE SEVENTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Wheel-Rail Contact Forces in High-Speed Simply Supported Bridges at Resonance
+Department of Structural Mechanics, Superior School of Civil Engineering, University of Granada, Spain
*Department of Structural Mechanics and Industrial Constructions, Superior School of Industrial Engineering, Technical University of Madrid, Spain
The present paper addresses the subject of the evolution of the wheel-rail contact forces during resonance situations in simply supported bridges. Based on a dimensionless formulation of the equations of motion presented in [4], very similar to the one introduced by Klasztorny and Langer in [3], a parametric study is conducted and the contact forces in realistic situations analysed in detail. The effects of rail and wheel irregularities are not included in the model.
The bridge is idealised as an Euler-Bernoulli beam, while the train is simulated by a system consisting of rigid bodies, springs and dampers. The situations such that a severe reduction of the contact force could take place are identified and compared with typical situations in actual bridges. To this end, the simply supported bridge is excited at resonace by means of a theoretical train consisting of 15 equidistant axles. The mechanical characteristics of all axles (unsprung mass, semi-sprung mass, and primary suspension system) are identical.
This theoretical train permits the identification of the key parameters having an influence on the wheel-rail contact forces. In addition, a real case of a 17.5 m bridges traversed by the Eurostar train is analysed and checked against the theoretical results.
The influence of three fundamental parameters is investigated in great detail: a) the ratio of the fundamental frequency of the bridge and natural frequency of the primary suspension of the vehicle; b) the ratio of the total mass of the bridge and the semi-sprung mass of the vehicle and c) the ratio between the length of the bridge and the characteristic distance between consecutive axles.
The main conclusions derived from the investigation are:
- The wheel-rail contact forces undergo oscillations during the passage of the axles over the bridge. During resonance, these oscillations are more severe for the rear wheels than for the front ones.
-
If
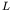 denotes the span of a simply supported bridge, and
denotes the span of a simply supported bridge, and 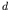 the
characteristic distance between consecutive groups of loads, the lower the value of
the
characteristic distance between consecutive groups of loads, the lower the value of
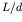 , the greater the oscillations of the contact forces at resonance. For
, the greater the oscillations of the contact forces at resonance. For 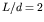 or greater, no likelihood of loss of wheel-rail contact has been detected.
or greater, no likelihood of loss of wheel-rail contact has been detected.
-
The ratio between the frequency of the primary suspension of the vehicle and
the fundamental frequency of the bridge is denoted by
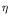 (frequency ratio), and
the ratio of the semi-sprung mass of the vehicle (mass of the bogie) and the total
mass of the bridge is denoted by
(frequency ratio), and
the ratio of the semi-sprung mass of the vehicle (mass of the bogie) and the total
mass of the bridge is denoted by 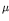 (mass ratio). For any given frequency ratio,
the greater the mass ratio, the greater the oscillations of the contact forces at
resonance.
(mass ratio). For any given frequency ratio,
the greater the mass ratio, the greater the oscillations of the contact forces at
resonance.
-
The oscillations of the contact forces at resonance, and therefore the likelihood
of loss of wheel-rail contact, present a minimum for
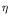 approximately between
0.5 and 1. For lower or higher values of the frequency ratio the oscillations of the
contact forces increase.
approximately between
0.5 and 1. For lower or higher values of the frequency ratio the oscillations of the
contact forces increase.
- Neglecting the possible effects of torsional vibrations, the metal or composite bridges with a low linear mass have been found to be the ones where the contact forces may suffer the most severe oscillations. If single-track, simply supported, composite or metal bridges were used in high-speed lines, and damping ratios below 1% were expected, the minimum contact forces at resonance could drop to dangerous values. Nevertheless, this kind of structures is very unusual in modern high-speed railway lines.
- 1
- European Rail Research Institute (D-214 Committee), "Ponts-Rails pour vitesses >200 km/h. Rapport Final." Rep. No. 9, Utrecht, 2001 (in French)
- 2
- L. Fryba, J. Naprstek, "Appearance of resonance vibration on railway bridges", in Advances in Civil and Structural Engineering Computing for Practice, 377-382, Civil-Comp Press, 1998. doi:10.4203/ccp.56.10.2
- 3
- M. Klasztorny, J. Langer, "Dynamic response of single-span beam bridges to a series of moving loads", Earthquake Engineering and Structural Dynamics, 19, 1107-1124, 1990. doi:10.1002/eqe.4290190803
- 4
- P. Museros, E. Alarcón. "An investigation on the importance of train- bridge interaction at resonance", Proceedings of the 6th International Conference on Computational Structures Technology (CST 2002), 335-336, Civil-Comp Press, Stirling (Scotland), 2002. doi:10.4203/ccp.75.143
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)