
engineering & technology publications
ISSN 1759-3158
PROGRESS IN CIVIL AND STRUCTURAL ENGINEERING COMPUTING
Optimal Choice of Performance Index Parameters for Control Design of Seismically Excited Structures
+Department of Electrical and Electronic Engineering
*Department of Civil Engineering, College of Judea and Samaria, Ariel, Israel
#Institute for Structural Concrete and Building Technology, University of Leipzig, Germany
According to the modern approaches the performance index has a form of matrix norms [1,3,4,6]. These indexes do not directly describe the real optimization. An additional criterion is proposed in the current study in order to improve the performance index and to design a control system, providing more efficient control and yielding further decrease in structural response to earthquakes.
The performance index weighting matrices usually have a diagonal form and give different weights to the components of the control forces and the regulated variables vectors. These weights take into account different physical nature of the components and different requirements to their values. Generally the weighting matrices selection is based on engineering experience by a "trial and error" method.
A two-level optimization procedure is proposed in this study. The first one is with a known feedback control solution, and for the second one the feedback control solution is unknown. A "compromise" solution is to use the first criterion as a "working" criterion for the second one.
The working criterions contain some weighting parameters. Let define these
parameters by W. In this case the second criterion will be a function of weighting
parameters W of the first one. Thus the problem is reduced to a choice of ![]() , at
which the optimal control according to criterion
, at
which the optimal control according to criterion ![]() provides minimum value of the
criterion
provides minimum value of the
criterion
![]() . This approach enables application of numerical parametric
optimization methods. According to the proposed method, the optimal control
synthesis problem should be solved at each step. Depending on the purpose and
priorities of designing one of the criteria [7] or their combination, a direct
optimization criterion can be chosen.
. This approach enables application of numerical parametric
optimization methods. According to the proposed method, the optimal control
synthesis problem should be solved at each step. Depending on the purpose and
priorities of designing one of the criteria [7] or their combination, a direct
optimization criterion can be chosen.
In order to demonstrate the affectivity and to verify the proposed optimization procedure, MATLAB - based optimum searches and simulations were carried out. A typical six-story steel office building [2] designed with UBC-73 has been chosen for the analysis. The structural system consists of a premier welded steel frame. Steel ASTM A36 was used for all shapes of columns and grids.
According to the results, applying the velocity and acceleration feedback control yields a reduction of up to 40% in the inter-story drifts and floor accelerations, compared to the uncontrolled structure. Applying the proposed method yields an additional decrease in inter-story drifts and floor accelerations (up to 43% and 67%, respectively), compared to the uncontrolled structure. The required control energy for the proposed method is lower for all the earthquakes, except the Hachinohe one, for which the increase in the required energy is very small, compared to the structural response improvement. Hence, the proposed strategy is very attractive for practical applications in structures designed to withstand earthquakes.
- 1
- P.J. Antsaklis, A.M. Mitchel, "Linear Systems", McGraw-Hill, 1997.
- 2
- D'Amore, Astanen - Asl, "Seismic Behavior of Six-story Instrumented Building under 1987 and 1994 Northridge Earthquakes", Report No. UCB/CE - Steel 95/03, Department of Civil Engineering, University of California, Berkeley, 1995.
- 3
- J.C. Doyle, K. Glover, P. Khargonekar, B. Francis, "State-space solutions to
standard
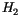 and
and 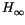 control problems", IEEE Transactions on Automatic
Control, 34:831-847, 1989. doi:10.1109/9.29425
control problems", IEEE Transactions on Automatic
Control, 34:831-847, 1989. doi:10.1109/9.29425
- 4
- S.J. Dyke, B.F. Spencer Jr., P. Quast, M.K. Sain, D.C. Kaspari Jr., and T.T. Soong, "Acceleration Feedback Control of MDOF Structures", J. Engrg. Mech., ASCE, Vol. 122(9), 897-971, 1995. doi:10.1061/(ASCE)0733-9399(1996)122:9(907)
- 5
- P.E. Gill, W. Murray, and M.H. Wright, "Practical Optimization", Academic Press, London, 1981.
- 6
- B.F. Spencer Jr., J. Suhardjo, and M.K. Sain, "Frequency Domain Optimal Control for Aseismic Protection", J. Engrg. Mech., ASCE, Vol. 120(1), 135-159, 1994. doi:10.1061/(ASCE)0733-9399(1994)120:1(135)
- 7
- B.F. Spencer, Jr., R.E. Christenson, S.J. Dyke, "Next generation benchmark control problem for seismically excited buildings", Proceedings of the Second World Conference on Structural Control, John Wiley & Sons, Chichester, England; New York, 2, 1351-1360, 1999.
purchase the full-text of this chapter (price £20)
go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £85 +P&P)