Keywords: free-surface flow, adaptive methods, front tracking, phase field method.

Free-surface flows are fundamentally important across a wide range of engineering problems from the spreading and deposition of viscous fluids to the production and control of droplets or the modelling and prediction of phase change. The nature of these free-surface flows varies significantly across and so an equally wide variety of computational methods have been developed for the accurate and efficient numerical simulation of such flows. In this talk a discussion a number of state-of-the-art computational techniques will be presented, based upon the experience of the author with his co-workers. The unifying theme will be the use of adaptive methods, with two distinct forms being considered: mesh movement and refinement-derefinement.

Figure 1 provides an illustration of results obtained using a mesh movement algorithm for a 3-d free-surface problem. This example is a liquid bridge problem in which an initially cylindrical mass of viscous fluid (left) lies between two flat circular faces at the top and bottom. The top face is then slowly moved upward and away from the bottom face whilst a gravitational force is applied in the opposite direction. In order to reach the state that is shown (right) a combination of mesh movement and a small number of discrete remeshing steps has been used.

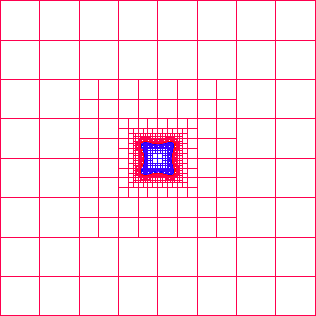
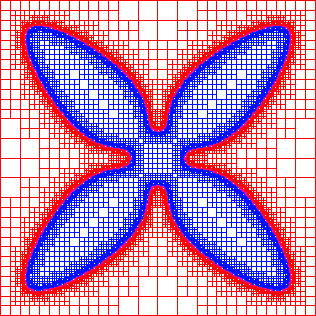
The results shown in Figure 2 illustrate the use of an adaptive algorithm based upon local mesh refinement and derefinement. The problem being solved is a two-dimensional phase-field model for the growth of a dendritic structure during the rapid solidification of a pure melt. The actual computational domain is larger than pictured but for the sake of clarity only the central region is shown. The adaptive algorithm that has been used is based upon a quad-tree data structure whereby each element, apart from those on the coarsest mesh, has a parent and either zero or four children. Those elements with no children are the leaf elements of the structure and are the elements that form the computational grid. Refinement can take place by subdividing a leaf element into four children, whilst derefinement consists of replacing a group of four sibling leaf elements by their parent (which now becomes a leaf element).

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)