
engineering & technology publications
ISSN 1759-3158
INNOVATION IN ENGINEERING COMPUTATIONAL TECHNOLOGY
Fractional Models: Sub and Super-Diffusives, and Undifferentiable Solutions
Department of Mathematical Analysis, Faculty of Mathematics, University of La Laguna, Tenerife, Spain
The main reason behind the usefulness of fractional derivatives in the close link that exists between fractional models and the "Jump" stochastic models, such as the continuous time random walk (CTRW) method, or those of the multiple trapping model type, such as Levy stable distributions and the generalisation of the central limit theorem. Since the second half of the 20th century, the CTRW method has been practically the only tool available to describe sub or super-diffusive phenomena associated with various complex systems. On the other hand, we note that fractional operators allow us to take the memory and non-locality properties of many anomalous processes into account.
In the second part of this paper we briefly present some fractional operators, along with their properties, which will allow us, from a very formal standpoint, to give examples of fractional models with boundary conditions. This should prove helpful in explaining why certain fractional derivative operators are well suited to modelling the dynamics of sub and/or super-diffusive phenomena.
Specifically, consider the well-known uni-dimensional problem associated with, for
example, the diffusion of heat in an isolated bar of unit length whose extremities are
kept at zero, with a diffusivity constant
![]()
We know the solution ![]() is given by
is given by
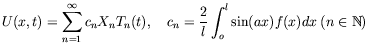 |
(3) |
with
| (4) |
Said solution ![]() clearly varies in time according to:
clearly varies in time according to:
![]() .
It then
decays in time like an ordinary negative exponent. We must then ask: what would
we have to do if we wanted the solution to the diffusion problem to proceed in time
at an extremely slower rate? What would its analytical differential model be like?
One simple approach would be to replace
.
It then
decays in time like an ordinary negative exponent. We must then ask: what would
we have to do if we wanted the solution to the diffusion problem to proceed in time
at an extremely slower rate? What would its analytical differential model be like?
One simple approach would be to replace ![]() with a new function whose exponent
decays more slowly. To this end, we can choose either of the two exponential
functions
with a new function whose exponent
decays more slowly. To this end, we can choose either of the two exponential
functions
![]()
![]() or
or
![]() , with
, with
![]() . These generalised exponentials
are both Mittag-Leffler type functions and they decay more slowly as the parameter
. These generalised exponentials
are both Mittag-Leffler type functions and they decay more slowly as the parameter
![]() approaches 0. Moreover, they have the following properties with respect to their
corresponding Riemann-Liouville or Caputo fractional derivative,
respectively:
approaches 0. Moreover, they have the following properties with respect to their
corresponding Riemann-Liouville or Caputo fractional derivative,
respectively:
![]() and
and
![]() . Therefore, the
following sub-diffusive models hold:
. Therefore, the
following sub-diffusive models hold:
However, neither of them can model super-diffusive phenomena since both
exponentials stop behaving as a negative exponent when ![]() . So if we wish to
devise a super-diffusive model, we have to find another generalisation of the
exponential and another fractional operator. Note that since the generalised Liouville
operator
. So if we wish to
devise a super-diffusive model, we have to find another generalisation of the
exponential and another fractional operator. Note that since the generalised Liouville
operator
![]() has the property
has the property
![]() with respect to
with respect to
![]() , it follows that
, it follows that
![]() is a sub and super-diffusive model.
Note that the previous models are easily generalised for the three-dimensional case
if, in the second term, the second order spatial derivative is replaced with the
corresponding Laplacian.
is a sub and super-diffusive model.
Note that the previous models are easily generalised for the three-dimensional case
if, in the second term, the second order spatial derivative is replaced with the
corresponding Laplacian.
Lastly, we use some examples based on Weierstrass functions to demonstrate the possibilities fractional models offer for simulating the dynamics of anomalous processes, which classical ordinary models do not.
purchase the full-text of this chapter (price £20)
go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)