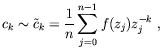Keywords: orthogonal Laurent polynomials on the unit circle, Fourier expansion, Szego quadratures, interpolation process.

Let be a complex function defined on the unit circle and consider its Fourier series , where

One of the most usual techniques with excellent results in the estimation of integrals (1) is the Trapezoidal rule:

where are the -th roots of the unit. The efficient computation of the coefficients has given rise to the well known algorithm of the Fast Fourier Transform (FFT) whose basic theoretical background is the following result: "Let be the unique polynomial of degree at most, interpolating at the -th roots of unity. Then, with given by 2 for ".

We start by showing that the above result and the relations (2) arise in a more general context, considering a weight function on and a sequence of orthogonal Laurent polynomials on with respect to and a general "generating sequence" [1]. The "generalised Fourier series expansion" for a function is given by where

(as usual, , ). Now, the calculation of the coefficients implies the computation of weighted integrals on the unit circle, and since the weight function can exhibit singularities near , the Trapezoidal rule seems to be unadvisable. In this work, more general procedures than the Trapezoidal rule are proposed in connection with the so called "Szego quadrature formulas" [2]. Such formulas are revisited, considering characterization results (for the nodes, weights and domains of exactness), error estimations and a convergence result.

The next purpose is concerned with the calculation of the Fourier coefficients of functions with polar singularities, that is, with functions of the form , which is a polynomial with all its zeros not on but close to . Thus, for any integer we need to compute , where is soft enough in a domain containing and . In this respect, two situations are particulary analysed (a symmetric and a non-symmetric distribution of poles) and the Szego, interpolatory and Trapezoidal rules computed, showing with some numerical experiments that, as expected, both Szego and interpolatory rules give better results than the Trapezoidal one and that the results strongly depend on the "soft" part of the function whose Fourier coefficients we need to compute. From the computations it seems it can be also deduced that the number of coefficients which can be effectively computed is approximately .

Finally, the concepts of Fourier expansion and interpolation are related and a connection with the Gauss-Christoffel, Gauss-Radau and Gauss-Lobatto formulae are established. More precisely, we shall be concerned with interpolation properties for real functions either -periodic by means of trigonometric polynomials or not periodic by means of algebraic polynomials taking as interpolation nodes the roots of . Moreover, some results of interpolation on intervals of the real line are deduced and a convergence result established. Here, the interpolation nodes are zeros of orthogonal polynomials with respect to the Chebyshev-type weight functions, namely where .

1

R. Cruz-Barroso, L. Daruis, P. González-Vera and O. Njåstad, "Sequences of orthogonal Laurent polynomials, bi-orthogonality and quadrature formulas on the unit circle", Journal of Computational and Applied Mathematics (To appear).

2

W.B. Jones, O. Njåstad and W.J. Thron, "Moment theory, orthogonal polynomials, quadrature, and continued fractions associated with the unit circle", Bull. London Math. Soc., 21, 113-152, 1989. doi:10.1112/blms/21.2.113

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)