
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Recovery of the Velocity and the Shape of the Interface of a Geological Layer
1National Institute for Research in Computer Science and Control (INRIA), Rennes, France
2American University of Beirut, Lebanon
We start first by presenting the mathematical model of the forward problem represented by the Eikonal equation:
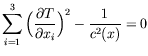 |
(88) |
We show how a well established result for this equation can be derived from the wave equation. Then the method of characteristics used to solve this equation is brieflydetailed. The aim of this method is to find a curve called, the characteristic, connecting the source to the receiver and along which the Eikonal equation is transformed into a system of ODEs called a characteristic system. So the unknown travel time can be computed using a simple formula of quadrature. Solving the forward problem using the method of characteristics is done by a specific code named ANRAY. To run a simulation with this code, the density and the wave velocity of each layer have to be specified as well as the position of the source and the receivers. Cubic B-splines are used to interpolate the interfaces and velocity fields.
In our two-dimensional inverse problem model, only one source and eight receivers are considered, so eight shots in total. The interface is defined by the depth of 30 points evenly spaced along the x-axis and the field velocity by a regular mesh. Many domain sizes have been tested with many different forms of interfaces. The inverse problem consists of minimizing the non linear mean square error function:
| (89) |
where
A sensitivity analysis is carried out to determine the maximal acceptable error added to the travel time measurements above which the solution is not reliable. We denote F, the forward problem operator, ![]() its Jacobian matrix, s the vector of singular values of
its Jacobian matrix, s the vector of singular values of ![]() and
and
![]() the relative error in the travel time measures. We show that in order to have all the parameters of the solution identifiable, the following relationship must hold:
the relative error in the travel time measures. We show that in order to have all the parameters of the solution identifiable, the following relationship must hold:
| (90) |
So we can deduce that the threshold of error is
We show in this paper a method to obtain the velocity field and the shape of the interface of a geological layer from a small number of travel time measures corresponding to a refracted seismic rays. The cost of the computations is affordable and solutions with good accuracy have been obtained. A sensitivity analysis has been made to justify the level of noise added to the measurements.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)