Fractures of some scale are present in all geological formations. Mapping and characterization of three-dimensional fracture networks is practically difficult. Stereological techniques have been used to derive three-dimensional descriptions from one and two-dimensional measurements, but the problems are usually ill-posed in the sense that the data cannot be inverted in a unique manner.

This study discusses stereological analysis of fracture networks observed in cylindrical galleries and the statistical characteristics of intersections between these galleries and fracture networks.

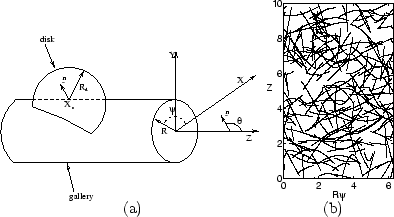
Fractures are assumed to be disks characterized by their radius R_d, orientation n, and center location X_c. Disk centers and orientations are assumed to be uniformly distributed. Fracture density is defined as the number of fractures per unit volume. This is illustrated in Figure 1.

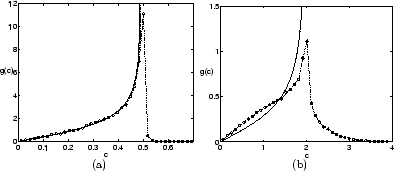
The number of intersections between the network and the gallery was determined in an exact way. The full intersections where a full ellipse is obtained, are also calculated. Approximations to these quantities based on a simple geometric argument are derived. Exact and approximate expressions are shown to agree well with Monte Carlo calculations.

Trace lengths are also analysed. The general case is presented; of course, the resulting formulae cannot be analytically integrated. Two simple cases are successively addressed when the disk normal is parallel to the cylinder axis and when the disk radius is much smaller than the gallery radius. Results are illustrated in Figure 2.

Systematic Monte Carlo calculations are finally given for monodisperse disks, polydisperse disks distributed according to power law, lognormal and exponential probability densities.

Figure 1: Intersection between a disk and the gallery (a) and the resulting traces for a monodisperse population of disks (b).

Figure 2: The trace length probability densities for randomly oriented monodisperse disks. In a and b, data are for: R=1, L=10 and N=10⁶: numerical simulation (), disk-plane (solid line), theoretical formula (dashed line); note that the dashed line is almost perfectly superposed onto the solid line. r_d= 0.25 (a), 1 (b).

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)