Keywords: h-adaptivity, iterative solver, domain decomposition, hierarchical structure, incomplete Cholesky factorization, preconditioned conjugate gradient method.

A previous paper [1] showed that the terms used to evaluate element stiffness matrices of geometrically similar finite elements are related by a constant, which is a function of the ratio of element sizes (the scaling factor). This geometrical similarity appears in h-adaptive refinements based on element splitting. This and other parent-child relations were used in a basic implementation of a hierarchical two-dimensional h-adaptive finite element code, based on element subdivision, for linear elasticity problems. The program uses a hierarchical data structure that significantly reduces the amount of calculations required for the evaluation of the problem stiffness matrix, stresses, error estimation, etc. The h-adaptive refinement process based on an element splitting produces a natural decomposition of the domain which, together with the hierarchical data structure of the program, directly produces an arrow-head stiffness matrix, shown in Figure 1, allowing for a decomposition of the global problem into smaller problems.

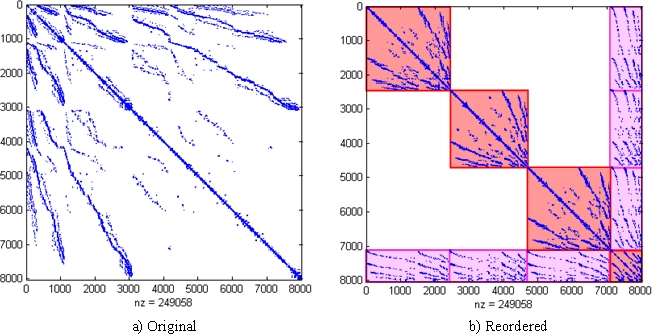
The system matrix is symmetric and positive definite, therefore the preconditioned conjugate gradient method (PCG) [2] is one of the most efficient available iterative methods. One of the preferred preconditioners is the incomplete cholesky factorization method (IC) [3]. This paper will consider a PCG method using an IC over the original un-reordered stiffness matrix as a reference method that will be compared to two different preconditioning strategies that make use of the block structure. The first strategy, denoted by , consists of computing the preconditioner using the main diagonal blocks of the reordered matrix. The second strategy, denoted by K, consists of evaluating the preconditioner using the whole reordered matrix.

Further numerical tests were run in order to check the effect that additional domain decompositions into the original subdomains would produce. The Matlab's command SYMAMD [4] was used to further transform the diagonal blocks into matrices with an arrowhead-like structure similar to those that would be directly obtained using nested domain decomposition into each of the original subdomains.

Memory requirements, associated with fill-in coefficients, and execution times have been considerably reduced with the proposed strategies. This memory requirement reduction allows bigger problems to be solved. The memory requirement reduction allows for the use of the K+additional Symamd reorder strategy even for small values of the threshold parameter considered in the evaluation of the preconditioner. This strategy has shown the better performance in the more refined meshes in all cases. This suggests the use of this strategy for finer meshes. The numerical tests presented in this paper show the importance of the use of further domain decompositions into the original subdomains.

1

J.J. Ródenas, J.E. Tarancón, J. Albelda, A. Roda, J. Fuenmayor, "Hierarquical properties in elements obtained by subdivision: a hierarquical h-adaptivity program", in Adaptive Modeling and Simulation 2005. P. Díez and N.E. Wiberg, (Editors), CIMNE, Sept. 2005.

2

M.R. Hestenes, E.L.Stiefel. "Methods of conjugate gradients for solving linear systems", Journal of Research of the National Bureau of Standards., Section B, 49, 409-436, 1952.

3

Y. Saad. "ILUT: a dual threshold incomplete ILU factorization", Numerical Linear Algebra with Applications, 1, 387?402, 1994. doi:10.1002/nla.1680010405

4

MATLAB, http://www.mathworks.com

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)