
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Efficient Preconditioners for Krylov Subspace Methods in the Solution of Coupled Consolidation Problems
Department of Mathematical Methods and Models for Scientific Applications, University of Padua, Italy
A consolidation problem is typically solved in space by a finite element (FE) technique giving rise to a system of first-order differential equations, the solution to which is usually addressed by an appropriate time marching scheme. A major computational effort is the repeated solution in time of the resulting discretized indefinite equations. In particular, with small time integration steps typically required in the early phase of the analysis the final linear system may be severely ill-conditioned [2], so that obtaining an accurate solution may prove difficult by any numerical approach.
Because of the large size of realistic three-dimensional (3-D) consolidation models (and particularly so in problems related to fluid withdrawal-injection from-into geological formations) the use of iterative solvers is generally recommended. Among them, projection (or conjugate gradient-like) methods based on Krylov subspaces for unsymmetric indefinite systems, such as Bi-CGSTAB are attracting a growing interest on the grounds of their robustness and efficiency. However, to accelerate convergence a key issue is the selection of an ad hoc efficient preconditioning strategy. The projection solver performance can be also improved by a proper preliminary left and right scaling which helps stabilize CG-like methods preconditioned by an incomplete triangular factorization.
The aim of the present paper is to investigate the performance and the robustness of a novel block preconditioner developed for the solution to the symmetric indefinite system of equations arising from the FE integration of the coupled consolidation equations.
At each time step, the solution of the linear system
![]() where
where
| (70) |
is performed by a Krylov subspace method, preconditioned by
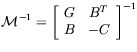 |
(71) |
with G a symmetric positive definite approximation of block K.
The eigenvalues of the preconditioned matrix are proven to be bounded
by the eigenvalues of ![]() .
.
Matrix G is either the diagonal or a sparse approximate inverse approximation of the (1,1) block K. Application of the preconditioner is performed via the Schur complement approach and the resulting Schur complement matrix is in its turn approximated by its incomplete Cholesky factorization. The preconditioner thus obtained is called inexact constraint preconditioner.
The outcome from two realistic medium and large size 3-D problems is compared to the solution strategy suggested by Gambolati et al. [3], which has proved to be, at present, one of the most effective solution techniques for large size, possibly ill-conditioned, FE coupled consolidation models. In particular, the comparison is performed for both normally conditioned and severely ill-conditioned problems.
Preliminary numerical results show that the inexact constraint preconditioners are flexible, robust and reliable tools for the iterative solution to FE consolidation models and possess a promising potential for further possible improvements.
- 1
- M. A. Biot, General theory of three-dimensional consolidation, J. Appl. Phys., 12 (1941), pp. 155-164. doi:10.1063/1.1712886
- 2
- M. Ferronato, G. Gambolati, and P. Teatini, Ill-conditioning of finite element poroelasticity equations., Int. J. Solids Struct., 38 (2001), pp. 5995-6014. doi:10.1016/S0020-7683(00)00352-8
- 3
- G. Gambolati, G. Pini, and M. Ferronato, Scaling improves stability of preconditioned CG-like solvers for FE consolidation equations., Int. J. Numer. Anal. Methods Geomech., 27 (2003), pp. 1043-1056. doi:10.1002/nag.311
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)