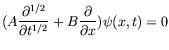Keywords: fractional differential equations, Riemann-Liouville fractional integrals and derivatives, Caputo fractional derivative, Mittag-Leffler and Wright functions, Dirac-type equations.

In this paper, we present a generalization of the linear one-dimensional diffusion and wave equations obtained by combining the fractional derivatives and the internal degrees of freedom associated with the system. Taking into account that the free Dirac equation is, in some sense, the square root of the Klein-Gordon equation, in a similar way we can operate a kind of square root of the time fractional diffusion equation in one space dimension through the system of fractional evolution-diffusion equations Dirac like. Solutions of the above system fulfils D'Alambert's formula as we demonstrate.

Following the well known Dirac's approach [2], it is possible to obtain his equation from the classical klein-Gordon equation. The free Dirac's equation is

where is a spinor, an structure that describes the state of the system and A and B are matrices satisfying Pauli's algebra. In fact this equation can be considered as a square root of the Klein-Gordon wave equation

where u is a scalar field.

As can be suspected, this relationship between both equations results in highly interesting to define roots of known operators. In the above context, Vázquez et al. recently considered in [1,3,4] the fractional diffusion equations with internal degrees of freedom. They can be obtained as the s-roots of the standard scalar linear diffusion equation. Thus, a possible definition of the square root of the standard diffusion equation (SDE) in one space dimension

is the following:

where A and B are matrices satisfying Pauli's algebra

being I the identity operator.

Here is a multicomponent function with at least two scalar space-time components. Also, each scalar component satisfies the SDE. Such solutions can be interpreted as probability distributions with internal structures associated with internal degrees of freedom of the system. They are named diffunors in analogy with the spinors in quantum mechanics.

We deal with a further generalization of Dirac's method. Concretely, we study the system of fractional evolution equations

with and where A and B are the same matrices as before satisfying Pauli's algebra.

We also make a mechanical formulation of the problem and we are able to obtain a conserved quantity, a fractional analogous to the classic hamiltonian.

1

T. Pierantozzi, L. Vázquez, "An interpolation between the wave and diffusion equations through the fractional evolution equations Dirac like". Journal of Mathematical Physics, 46, 113512, 2005. doi:10.1063/1.2121167

2

S. S. Schweber, "An Introduction to Relativistic Quantum Field Theory", Harper Int. Ed. New York, 1966.

3

L. Vázquez, "Fractional diffusion equation with internal degrees of freedom", J. Comp. Math., Vol. 21, n. 4, 491-494, 2003. doi:10.1016/S0096-3003(02)00326-0

4

L. Vázquez, R. Vilela Mendes, "Fractionally coupled solutions of the diffusion equation", Applied Mathematics and Computation, 141, 125-130, 2003. doi:10.1016/S0096-3003(02)00326-0

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)