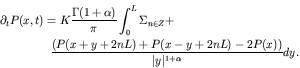Keywords: space-fractional diffusion, Lévy flights, impermeable boundaries, bound domain.

Field and laboratory experiments indicate that in heterogeneous porous media, the spreading of matter may be described by long-tailed non-Gaussian statistics. Such results would be impossible if the spreading of matter were ruled by the classical diffusion equation. More general, so-called fractional models, were proposed for such situations, but little attention was paid to the influence of boundary conditions. Since in practical situations and experiments we frequently have to consider bounded domains, but fractional derivatives are non-local operators, so introducing boundary conditions may be non-obvious. Here we focus on fractional diffusion in a domain, bounded by reflective walls.

A small scale model for diffusive transport behavior is based on the continuous time random walk approach. Space-fractional diffusion equations were shown to represent the diffusive limit of a wide class of uncoupled continuous time random walks which contains symmetric Lévy flights. In the latter model the spreading of many particles, performing successive independent jumps whose length is a random variable, are distributed according to a stable Lévy law. Jumps are separated by waiting times, which also are independent identically distributed random variables, whose mean does exist. Brownian motion is a limiting case; the concentration of a cloud of particles performing such a random walk evolves according to the classical diffusion equation. Lévy stable laws of index for the jump length correspond, at macroscopic level, to evolution partial differential equations, which are slightly more general: the Laplacean may be replaced by a fractional derivative (with respect to space) of order between 0 and . Such operators are non-local and account for long range interactions. The above mentioned non-Gaussian statistics correspond to solutions fractional equations obtained, just as Gaussian distributions solve the classical diffusion equation. Gaussian statistics and ordinary diffusion correspond to the limiting case .

The above cited results were stated for infinite domains. Impermeable boundaries were shown to correspond to a non-trivial modification of the macroscopic model, in the case of a semi-infinite domain. In the same spirit, the diffusive limit of Lévy flights in a bounded medium, limited by two reflective walls, takes a slightly different form.

Consider particles, being in at instant , and performing an uncoupled CTRW. Then, the probability of finding a particle in at instant t is , with satisfying the generalized master equation

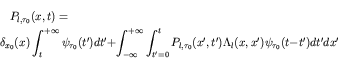
Here is the p.d.f. of the waiting time between successive jumps , while a particle which jumps from arrives in with probability . With two elastic barriers, due to possible multiple bounces against the walls, is

Indeed, a jump from to x , hitting the wall in once, has length . Jumps involving n bouncings on both walls have length or . Meeting the walls in and respectively and n times, implies a length . The reverse yields .

When and tend to zero and satisfy , the limit of satisfies

Adapting a numerical scheme, borrowed from the infinite media case and tested against exact solutions, then allows us to display solutions to (19), obtained for several values of . Comparisons with Monte-Carlo simulations of Lévy flights "with walls" illustrate the above result, and we can see that decreasing significantly increases the rate, leading to equilibrium.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)