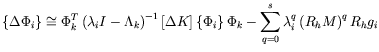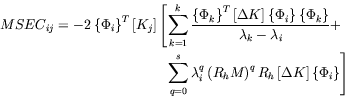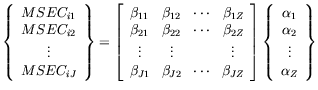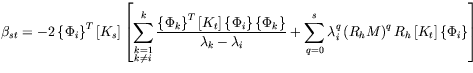engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
An Improved Structural Damage Detection Method Based on Modal Strain Energy
1Civil Engineering and Architecture College, Central South University of Forestry and Technology, Changsha, Hunan, P.R.China
2Department of Civil and Environmental Engineering, Lulea University of Technology, Sweden
According to the structural modal methods, with a change of stiffness and mode shape, it can be assumed that,
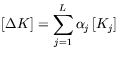 and and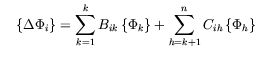 |
(60) |
where,
The total contribution of lower and higher modes can be expressed as follows,
The modal strain energy change (MSEC) of the
Substituting equation (61) into equation (62)
Selecting the values of MSE of
Coefficient
This approach could be applied to detect structural damage location and quantity by using only the first one or two modes.
The three numerical examples with different structures, but the same damaged case, are studied in present. The results illustrate that the present method is simple and effective with satisfactory precision both in locating the place of damage and estimating the magnitude of damage. The following conclusions have been obtained:
- The damage localization method presented in this paper needs only one or two lower modes in order to obtain satisfactory results.
- The damage quantification method developed in this paper is practical and simple. The modal truncation error can be ignored even if only one or two lower modes used.
- In order to obtain the better precision, the coefficient
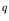 can be taken nonzero,
i.e., the influence of dynamic contribution of higher modes is considered.
can be taken nonzero,
i.e., the influence of dynamic contribution of higher modes is considered.
- When measured DOFs are incomplete in practice, it can be expanded using a mode shape expansion method.
- 1
- A.K. Pendey, M. Biswas and M.M. Samman, "Damage Detection from Changes in Cuvature Mode Shapes", Journal of Sound and Vibration, 145(2), 1991. doi:10.1016/0022-460X(91)90595-B
- 2
- O.S. Salawn and C. Williams, "Damage Location Using Vibration Mode Shapes", Proc. of the 12th IMAC, 933-939, 1994.
- 3
- N. Stubbs, "Clobal Non-Destructive Damage Evaluation in Solid", International Journal of Analytical and Experimental Modal Analysis, 5(2), 1990.
- 4
- T.Y. Chen and J.A. Garba, "On-Orbit Damage Assessment for Large Space Structures", AIAA Journal, 26(12) , 1998. doi:10.2514/3.10019
- 5
- N.A.J. Lieven and D.J. Ewins, "Error Location and Updating of Finite Element Models Using Singular Value Decomposion", Proc.of the 8th IMAC, 768-773, 1990.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)