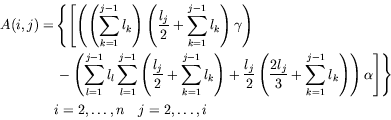Keywords: modal analyses, damage, identification, dynamics, experiments, simulations.

This study presents a theoretical methodology that might be applied in order to evaluate the existing mechanical damage that affects beams, in the case of bridges, for example. The application of this method is based on the knowledge of the system mass matrix and two experimental eigenvalues of the modal frequency and the corresponding modal shapes. Dynamic tests are performed on simply-supported metallic beams. Actually, during free vibration tests, the structural response is measured in terms of structural accelerations. These accelerations are processed with an existing methodology and the modal frequencies and the corresponding modal shapes are therefore derived. The preliminary damage, before tests, is due to an adopted area reduction. Various damage conditions are tested: In Figure 1 up to three areas are damaged among the five possible sections.

The theoretical methodology proposed in this paper allows therefore the assessment of the structural damage that affects the beam. The theoretical developments are described, in the present study. Actually, the "experimental" eigenvectors should be corrected in order to guarantee the orthogonality between the modes and also the orthogonality with the mass matrix, this latter being known.

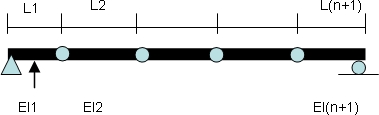
For the beam shown in Figure 1, the flexibility matrix, mass matrix, and the two eigenvalues are substituted into the equilibrium dynamic equation

After various algebraic steps described in the paper, one obtains a linear system:

where the vector expresses the "stiffness" values, , for each of the constitutive sections shown in Figure 1. Some of the values of the matrix and the vector give the following:

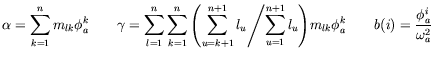with = length span , the mass coefficient, coordinate of eigenvector , and modal frequency .

Free vibration tests are performed by applying initial displacement or initial velocity conditions to one wide flanged beam, of 4 meters in length. The simply-supported beam was theoretically divided into five constitutive sections, each having the same length. Acceleration was measured at different points on the beam (four locations in the present study). One of up to three cross sections (at mid-length of the constitutive sections) was therefore damaged as their area is reduced. Accelerations are measured with four different damage conditions:

• When the beam remains still undamaged
• When the damage affects the second section
• When the damage affects the second and third sections
• When the damage affects second, third and fourth sections

From the experimental structural response, the modal shapes and the modal frequencies ( and ) are derived for each set of the damage conditions. The theoretical methodology provides therefore the mechanical damage value for each of the constitutive sections, Eqns. (58-59). This damage expresses that variation of the initial flexural stiffness . The obtained damage, for the tested beam, varies from 0 up to 40%. One should however notice that the damaged stiffness should not be larger than the initial stiffness , since the sections are not strengthened.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)