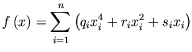Keywords: conjugate gradients, optimisation, quasi-Newton, structural.

This paper is concerned with assessing the performance of a combined conjugate gradient and quasi-Newton method for a number of relatively simple non-linear structural optimisation problems. The problems considered are designed to be poorly conditioned as the new method is shown to be particularly adept at solving these types of problems. The features of the new method are quadratic termination and that matrix updating is present, similar to the quasi-Newton method. However, this latter feature is optional and if no updating takes place the method reduces to the standard conjugate gradient method whilst if full updating is performed the quasi-Newton method is obtained. It is shown in the paper that best performance is obtained with partial updating and the extent depends on the ill-conditioning of the problem.

All of the modern iterative methods display poor performance when applied to very poor conditioned systems. This has led to the investigation into the use of self-preconditioning and hybrid solvers (see Saad for example). Most successful modern methods are based on some form of successive orthogonalisation of Krylov type spaces combined with some minimisation step. Although these methods are excellent linear equation solvers they suffer some disadvantages when applied to non-linear systems arising in design optimisation. A typical approach might be to combine these methods with a Newton method to give inexact Newton methods. However, the link between the linear solver and the Newton method is tenuous with little useful information being passed between the solvers.

In this paper a new approach is proposed which essentially combines the preconditioned conjugate gradient method (PCGM) with the quasi-Newton method. The method can be classified as an inexact Newton method but has the added feature that the preconditioner developments over linear and non-linear iterations. The method can also be applied directly for function minimization. The method is founded on the ideas of Davey and Ward and has similarities with the method of van der Vorst and Vuik, which is founded on rank-one matrix updates, and that of Axelsson and Vassilevski. The new features of the proposed method are: the linkage with quasi-Newton methods, the use of rank-two updates, and preconditioners developing over linear and non-linear iterations. Particular focus in this paper is on the use of direct approximations to the inverse Hessian matrices that are generated by the method.

A relatively simple non-linear problem is considered here and consists of the minimisation of

where and are sequences of pseudo-random number between 0 and 1, for , and between 0 and 10 for , and is a sequence of pseudo-random numbers between 0 and 1. In order to produce fully populated systems minimisation is performed with respect to where , and where the matrix is an orthogonal matrix generated as a product of individual orthogonal matrices .

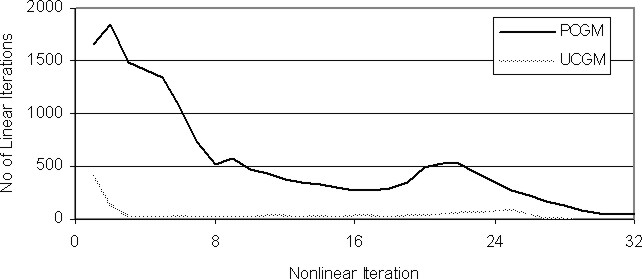
The results for problem (32) with and are presented in Figure 1. As the non-linear scheme progresses, the potential of the UCGM schemes becomes clear in terms of reducing the number of linear iterations required. It is interesting to observe the ability of the UCGM to keep the number of linear iterations to convergence at a low level.

This paper is concerned with the development of the updating conjugate gradient method for the minimisation of non-linear functions that are sufficiently smooth to possess a continuous Hessian. The following conclusions can be made:

• The updating CGM can utilise BFGS updates to precondition over linear and non-linear iterations.
• If applied as an inexact Newton method the UCGM stabilises the number of linear iterations per non-linear iteration.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)