
Computational & Technology Resources
an online resource for computational,
engineering & technology publications
engineering & technology publications
Civil-Comp Proceedings
ISSN 1759-3433
ISSN 1759-3433
CCP: 83
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Edited by: B.H.V. Topping, G. Montero and R. Montenegro
Paper 175
Reordering for the Iterative Solution of Hybrid Elastic Structures
A. Comerlati, G. Gambolati and C. Janna
Department of Mathematical Methods and Models for Scientific Applications (DMMMSA), University of Padova, Italy
Full Bibliographic Reference for this paper
A. Comerlati, G. Gambolati, C. Janna, "Reordering for the Iterative Solution of Hybrid Elastic Structures", in B.H.V. Topping, G. Montero, R. Montenegro, (Editors), "Proceedings of the Eighth International Conference on Computational Structures Technology", Civil-Comp Press, Stirlingshire, UK, Paper 175, 2006. doi:10.4203/ccp.83.175
Keywords: reordering, Krylov, preconditioning, conjugate gradient.
Summary
It is well known that the outcome of the finite element method in linear elastic
structural problems is a linear system with the system matrix both
symmetric and positive definite (SPD) [1,2].
In the present paper, the influence of matrix reordering on
convergence of the preconditioned conjugate gradient (PCG) is addressed.
The two preconditioners used herein are a variant of the
incomplete Cholesky factorization with an user-specified
fill-in degree [3]:
- the former is a variant of the ILUT preconditioner [4,3]
(here denoted as SAADILUT), which is commonly used for
nonsymmetric problems and firstly converts matrix
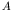 from the symmetric sparse row (SSR) to the compressed
sparse row (CSR) format;
from the symmetric sparse row (SSR) to the compressed
sparse row (CSR) format;
- the latter is an incomplete factorization with a variable fill-in (denoted as SYMILUT) that is implemented so as to take the maximum advantage from the matrix symmetry and not to require the format conversion from SSR to CSR.
As mentioned above our focus is on linear systems arising from the spatial discretization of linear elastic civil structures obtained by coupling different elements such as beams, trusses, and shells. The ordering schemes addressed are:
- SPARSKIT based on the Cuthill-McKee algorithm [5,3];
- METIS based on the multilevel nested dissection algorithm [6].
- when far nodes are connected, the native unknowns ordering yields SPD matrices which may not be suitable for the solution by PCG methods due to the poor preconditioner quality;
- Choleski-based symmetric preconditioners provide the best overall performance with matrices reordered with METIS;
- the direct solver MA57 outperforms the best PCG by a factor 3-4 and is more robust as it does not require the selection of any empirical parameter such as the most appropriate degree of fill-in in the preconditioner calculation.
References
- 1
- Bathe, K. L. (1996). Finite Element Procedures. Pretince-Hall. 1037 pp.
- 2
- Zienkiewicz, O. C. and Taylor, R. L. (2000). The Finite Element Method. 1: The basis, volume 1.
Butterworth and Heneimann, 5th edition. 689 pp. - 3
- Saad, Y. (2003). Iterative Methods for Sparse Linear Systems. SIAM, Philadelphia, PA.
- 4
- Saad Y. (1994). ILUT: A dual threshold incomplete ILU factorization. Num. Lin. Alg. Appl., 1, 387-402. doi:10.1002/nla.1680010405
- 5
- Saad, Y. (1990). SPARSKIT: A basic tool kit for sparse matrix computations. Technical Report 90-20, NASA Ames Research Center, Moffett Field, CA, Moffett Field, CA.
- 6
- Karypis, G. and Kumar, V. (1998). METIS. A software package for partitioning unstructured graphs, partitioning meshes, and computing fill-reducing orderings of sparse matrices. Version 4.0. University of Minnesota, Department of computer science / Army HPC research center, Minneapolis, MN 55455.
- 7
- HSL Archive - a catalogue of subroutines. (2004). Aea Technology, Engineering Software, CCLRC. http://www.cse.clrc.ac.uk/nag/hsl.
- 8
- Dongarra, J. J., Duff, I. S., Sorensen, D. C. and van der Vorst H. A. (1998). Numerical linear algebra for high-performance computers. SIAM, Philadelphia, PA.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)