
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
A Three Dimensional Semi-Analytical Finite Element Model for the Analysis of Piezoelectric Shells of Revolution
1IDMEC/IST - Instituto de Engenharia Mecânica, Instituto Superior Técnico, Lisbon, Portugal
2Department of Mechanical Engineering, Texas A&M University, Austin TX, United States of America
Physically, the piezoelectric effect was discovered when certain crystals produce electric charges by application of pressure, defined as the direct effect. This properties where discovered on late XIX century by Curie brothers. Allik and Hughes [1] presented a numerical method, using the finite element method, for three-dimensional analysis for piezoelectric media.
Recently, Kapuria, et al. [2] developed a three-dimensional solution for simply
supported piezoelectric cylindrical shells subjected to axisymmetric
electromechanical load. Mitchell and Reddy [3] made a study of the static behavior
using an approximate theory. Pinto Correia, et al. [4] developed a semi-analytical
axisymmetric shell finite element model with embedded and, or surface bonded
piezoelectric rings actuators and, or sensors for active damping vibration control of
the structure. Santos, et al. [5] developed a general semi-analytical finite element
model for bending, free vibration and buckling analysis of shells of revolution made
of laminated anisotropic elastic material. The 3D elasticity theory was used and the
equations of motion were obtained by expanding the displacement field and load in
the Fourier series in terms of the circumferential coordinate, ![]() . The primary
variables are represented by:
. The primary
variables are represented by:
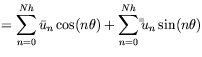 |
(22) | |
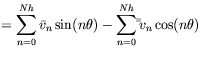 |
(23) | |
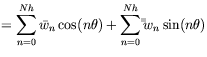 |
(24) | |
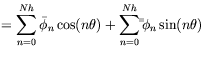 |
(25) |
where
This paper addresses the bending and free vibrations of multilayered cylindrical shells with piezoelectric properties using a semi-analytical axisymmetric shell finite element model with piezoelectric layers using the 3D linear elasticity theory. Thus, the 3D elasticity equations of motion are reduced to 2D equations involving circumferential harmonics. Special emphasis is given to the coupling between symmetric and anti-symmetric terms for laminated materials with piezoelectric rings. Numerical results obtained with the present model are found to be in good agreement with other finite element solutions.
- 1
- Allik H., Hughes T.J.R. "Finite element method for piezoelectric vibration", International Journal Numerical Methods in Engineering. 2: 151-157, 1970. doi:10.1002/nme.1620020202
- 2
- Kapuria S., Sengupta S., Dumir P.C. "Three-dimensional solution for simply-supported piezoelectric cylindrical shell for axisymmetric load", Computational Methods in Applied Mechanics and Engineering. 140: 139-155, 1997. doi:10.1016/S0045-7825(96)01075-4
- 3
- Mitchell J.A., Reddy J.N. "A refined hybrid plate theory for composite laminates with piezoelectric laminae", International Journal of Solids and Structures. 32(16): 2345-2367, 1995. doi:10.1016/0020-7683(94)00229-P
- 4
- Pinto Correia I.F., Mota Soares C.M., Mota Soares C.A., Herskovits J. "Active control of axisymmetric shells with piezoelectric layers: a mixed laminated theory with a high order displacement field", Computers and Structures. 80: 2265-2275, 2002. doi:10.1016/S0045-7949(02)00239-0
- 5
- Santos H., Mota Soares C.M., Mota Soares C.A., Reddy J.N. "A semi-analytical finite element model for the analysis of laminated 3D axisymmetric shells: bending, free vibration and buckling", Composite Structures. 71(3-4): 273-281, 2005. doi:10.1016/j.compstruct.2005.09.006
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)