Keywords: axisymmetric conical shells, piezoelectric laminates, finite elements, fluid-structure interaction, free vibrations.

In the context of active structural acoustic control problems, this work presents the theoretical formulation and the finite element implementation of piezoelectric composite shells of revolution filled with compressible fluid. The originality of this work lies (i) in the development of an inexpensive and accurate axisymmetric adaptive laminated conical shell element, and (ii) in the modal formulation of the fully coupled fluid-piezoelectric-structure system.

The piezoelectric shell, which is based on Kirchhoff-Love theory, is supposed to be polarized in the thickness direction. The associated finite element model combines an equivalent single layer approach for the mechanical behavior with a layerwise representation of the electric potential in the thickness direction. It can be noted that this relatively simple model can be enhanced using for example a single-layer higher order shear deformation theory [1]. The fluid is supposed to be inviscid, compressible and barotropic, gravity effects being neglected. Considering these assumptions, the fluctuating fluid forces are determined by means of the linearized Euler equations and reduced to the Helmholtz equation for the pressure. The dynamic formulation of the above described coupled system is derived from a variational principle involving shell displacements and rotation, electric potential and fluid pressure. It is important to note that the proposed variational formulation can be written in a symmetric form through the introduction of a displacement potential of the fluid [2].

Concerning the finite element discretization, a one-dimensional element with two nodes is used for the adaptive conical shell structure, and a quadrangular element with four nodes for the fluid. Moreover, an appropriate interface element is developed to ensure the interaction between fluid and structure. For the shell element, each node has (i) four mechanical degrees of freedom to describe axial, radial and circumferential displacements, as well as the rotation about the circumferential axis, and (ii) one electrical degree of freedom related to the sensor voltage per piezoelectric layer. For the fluid element, the pressure is the unique nodal unknown. It should be mentioned that the variables associated with these two elements are expanded in a Fourier series in the circumferential direction.

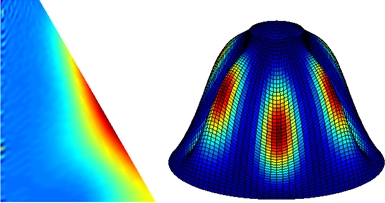
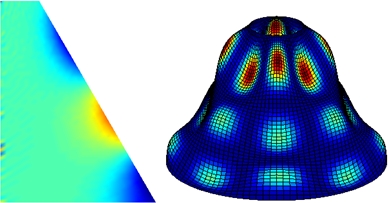
Finally, some numerical examples are presented in order to validate and demonstrate the effectiveness of the proposed formulation. For example, the free-vibration of a simply supported piezoelectric transversely isotropic cylinder completely filled with compressible fluid is analyzed and compared to a three-dimensional exact state space solution proposed by the authors [3]. Then, other examples concerning the vibration analysis of composite cylindrical or conical shells with internal fluid are detailed. For illustrative purposes, Figure 1 presents the first and third mode shapes of an axisymmetric truncated composite conical shell rigidly clamped at both ends and filled with air.

1

F. Pinto Correia, C.M. Mota Soares, C.A. Mota Soares and J. Herskovits, "Active control of axisymmetric shells with piezoelectric layers: a mixed laminated theory with a high order displacement field", Computers & Structures, 80(27-30), 2265-2275, 2002. doi:10.1016/S0045-7949(02)00239-0

2

Morand H.J.-P., Ohayon R., Fluid Structure Interaction, Wiley, New York, 1995.

3

Deü J.-F., W. Larbi, "A state space method for free-vibration analysis of radially polarized laminated piezoelectric cylinder filled with fluid", Proceedings of the Eighth International Conference on Computational Structures Technology, Civil-Comp Press, Stirling, UK, 2006. doi:10.4203/ccp.83.103

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)