
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE EIGHTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Modelling Frequency Adjustment Effects Using Shape Memory Alloy Oscillators
1MCI, Faculty of Science and Engineering, University of Southern Denmark, Sonderborg, Denmark
2Mathematical Modelling and Computational Sciences, Wilfrid Laurier University, Waterloo ON, Canada
In the present paper, we model the performance of a shape memory alloy oscillator used as a vibration absorber, which consists of a shape memory alloy rod and an end-mass. The vibration characteristic of the oscillator is continuously adjustable by changing its temperature, due to the thermo-mechanical coupling property of the shape memory alloy rod.
In order to capture the thermo-mechanical coupling property in the material, as well as
hysteresis induced by phase transformations at low temperature, the mechanical behaviour
of the SMA rod is first modelled using the modified Ginzburg-Landau theory by the
following partial differential equation:
| (19) |
where
For the convenience of the analysis, the above model is simplified. By taking into account the nature of the absorber, it can be approximated
by the following model. representing a force-deformation relation for a nonlinear spring:
| (20) |
where
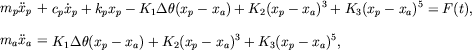 |
(21) |
The performance of the SMA oscillator used as a vibration absorber is then simulated numerically using the developed model. It is demonstrated that the SMA oscillator can be adjusted to match various vibration frequencies by changing its temperature. It is shown that at high temperature, the SMA oscillator has a similar behaviour with linear vibration absorbers and the vibration of the primary system can be suppressed to a rather small value. The frequency response of the SMA oscillator also indicates a certain similarity between the (nonlinear) SMA absorber and linear ones. It is also demonstrated that at low temperature, the SMA absorber can be used as a general vibration damper, because it is able to dissipate energy due to the hysteresis. However, the frequency response of the absorber exhibits in this case a much more complicated behavior compared to its linear counterpart.
- 1
- S.M.T. Hashemia, and S.E. Khademb, Modeling and analysis of the vibration behavior of a shape memory alloy beam, Inter. Jour. Mech. Sci. 48 (2006) 44-52. doi:10.1016/j.ijmecsci.2005.09.011
- 2
- S. Saadat, J. Salichs, M. Noori, Z. Hou, H. Davoodi, I. Bar-on, Y. Suzuki, and A. Masuda, An overview of vibration and seismic applications of NiTi shape memory alloy, Smart Materials and Structures, 11 (2002) 218-229. doi:10.1088/0964-1726/11/2/305
- 3
- K. A. Williams, G. T. C. Chiu, and R. J. Bernhard, Dynamic modelling of a shape memory alloy adaptive tuned vibration absorber. Journal of Sound and Vibration 280 (2005) 211-234. doi:10.1016/j.jsv.2003.12.040
- 4
- F. Falk, P. Konopka, Three-dimensional Landau theory describing the martensitic phase transformation of shape memory alloys. J.Phys.:Condens.Matter 2 (1990) 61-77. doi:10.1088/0953-8984/2/1/005
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £140 +P&P)