Keywords: optimisation, scissor-link foldable structures, design, uniplet, genetic algorithm.

The need for mobile, re-usable structures that are characterized by fast and easy erection existed for along time. Such structures found many applications in temporary constructions. The first such structure has been designed and constructed by Pinero. Substantial contribution to the general understanding of geometric and kinematic behavior of scissor-link structures is due to Escrig [1], Gantes et al [2], Shan [3], and Kaveh and Davaran [4], among many others. In structural engineering, Goldberg and Samtani [5], Rajeev and Krishnamoorthy [6], Jenkins [7], Lin and Hajela [8], Saka [9], Kaveh and Kalatjari [10,11,12] used genetic algorithm for optimisation. In this article, the genetic algorithm is employed to optimize scissor-link foldable structures. The advantage of using GA lies in the fact that the discrete spaces can be optimized without any complexity. Here, displacement method is used for analysis, employing uniplet elements.

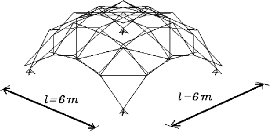
A genetic algorithm is employed to optimize scissor-link foldable structures. For justification of the developed algorithm, first a classical example of a 25-bar space truss is studied. Then, two foldable structures are optimised using the present algorithm. The first example is a 32-uniplet foldable barrel vault. Application of GA resulted in a structure with the wieght 817.38N (183.7lb). The second example is an 80-uniplet foldable dome as shown in Figure 1. In this example, the number of generation is taken as 50, the population size is chosen as 100, the mutation rate is 0.15, and the constant for penalty function is taken 3.6. The optimaization process leads to a dome with 2310.6 N (519.2 lb).

The main emphasis of this article is on the suitability of the genetic algorithm for the opimal design of foldable structures. The present algorithm, achieves optimal designs with a good convergence. The selection method prevents omitting the best individuals, and the considered high rate of mutation, reduces the chance of local optima. Finally, the use of uniplets simplifies the analysis of flodable structures and hence increases the efficiency of the optimisation process.

1

Escrig, F., "Expandable Space Structures", International Journal of Space Structures, 1, 79-91, 1985.

2

Gantes, C.J., Connor, Y., Rosenfeld, Y. and Logcher, R.D., "A Systematic Design Methodology for Deployable Structures", International Journal of Space Structures, Vol. 9, No. 2, 1994.

3

Shan, W., "Computer Analysis of Foldable Structures", Computers and Structures, No. 6, 42, 903-912, 1992. doi:10.1016/0045-7949(92)90102-6

4

Kaveh, A. and Davaran, A., "Analysis of Pantographic Foldable Structures", Computers and Structures, No. 1, 59, 131-140, 1996. doi:10.1016/0045-7949(95)00231-6

5

Goldberg, D.E. and Samtni,M.P., "Engineering Optimisation via the Genetic Algorithms", Computers and Structures, 40, 1321-1327, 1991. doi:10.1016/0045-7949(91)90402-8

6

Rajeev S. and Krishnamoorthy, C.S., "Genetic Algorithms-based Methodology for Design Optimisation of Trusses", J. Struct. Eng., ASCE, 123, 250-358, 1997. doi:10.1061/(ASCE)0733-9445(1997)123:3(350)

7

Jenkins, W.M., "Plane Optimum Design Environment Based on Genetic Algorithms", J. Struct. Engrg., ASCE, No.11, 121, 3103-3112, 1992. doi:10.1061/(ASCE)0733-9445(1992)118:11(3103)

8

Lin C.Y. and Hajela, P., "Genetic Algorithms in Optimisation Problems with Discrete and Integer Design Variables", Engrg. Opt., 19, 309-327, 1992. doi:10.1080/03052159208941234

9

Saka, M.P., "Optimum design of pitched roof steel frames with haunched rafters by Genetic algorithm", Computers and Structures, 81, 1967-1978, 2003. doi:10.1016/S0045-7949(03)00216-5

10

Kaveh, A. and Kalatjari, V., "Genetic algorithm for discrete sizing optimal design of trusses using the force method", International Journal of Numerical Methods in Engineering, 55, 55-72, 2002. doi:10.1002/nme.483

11

Kaveh, A. and Kalatjari, V., "Size/geometry optimisation of trusses by the force method and genetic algorithm", ZAMM, No.5, 84, 347-357, 2004. doi:10.1002/zamm.200310106

12

Kaveh, A. and Kalatjari, V., "Topology Optimisation of trusses using genetic algorithm, force method and graph theory", International Journal of Numerical Methods in Engineering, No.5, 58, 771-791, 2003. doi:10.1002/nme.800

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £95 +P&P)