Keywords: convex polyhedrons, natural element coordinates, quadrature formulas.

The finite element method is used to simulate processes in science, nature and engineering to solve descriptive partial differential equations. As geometrical basis of finite element method triangles and quadrangles in the 2-dimensional space are used as well as tetrahedrons and cubes in the 3-dimensional space. In this paper the use of any convex polyhedrons as finite elements is introduced.

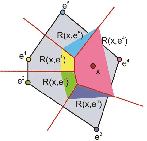
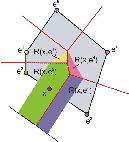
The formulation of a local coordinate system makes a uniform description of interpolation and test functions possible. In this paper natural element coordinates for any convex polyhedrons [1] will be introduced. It has been shown that natural element coordinates could be conceived as generalized barycentric coordinates. Every edge of the convex polyhedron can be matched a local coordinate .

To assess the natural element coordinate for a point the VORONOI-decomposition of first order and the VORONOI-decomposition of second order are drawn according the point .

The natural element coordinate can be compute by the ratio of the LEBESGUE-measure of the VORONOI-region and . The use of natural element coordinates enables a geometry independence formulation of interpolation and test functions [2].

In the case of finite element approximation [3] the differentiation and integration of these interpolations and test functions are necessary.

In this paper especially the properties of the natural element coordinates whose differential- and integration ability are brought to attention. The necessary methods and their numerical implementation are introduced and advantages and disadvantages are described.

Finally, applications from the range of interpolation of data and approximations of solutions of partial differential equations in field of mechanics are presented.

1

P. Milbradt, "Algorithmische Geometrie in der Bauinformatik", Habilitationsschrift, Universität Hannover, 2001

2

J. Schierbaum, A. Schwöppe, "Ansatzfunktionen höherer Ordnung für Finite konvexe Zellen", Forum Bauinformatik 2003

3

P. Milbradt, A. Schwöppe, "Finite Element Approximation auf der Basis geometrischer Zellen", IKM, Weimar 2003

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)