Computational & Technology Resources
an online resource for computational,
engineering & technology publications
engineering & technology publications
Civil-Comp Proceedings
ISSN 1759-3433
ISSN 1759-3433
CCP: 79
PROCEEDINGS OF THE SEVENTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
PROCEEDINGS OF THE SEVENTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Edited by: B.H.V. Topping and C.A. Mota Soares
Paper 87
Geometrical Approach to Two Degrees-Of-Freedom Mechanical System Dynamics
J. Awrejcewicz, D. Sendkowski and M. Kazmierczak
Department of Automatics and Biomechanics, Technical University of Lodz, Poland
Full Bibliographic Reference for this paper
J. Awrejcewicz, D. Sendkowski, M. Kazmierczak, "Geometrical Approach to Two Degrees-Of-Freedom Mechanical System Dynamics", in B.H.V. Topping, C.A. Mota Soares, (Editors), "Proceedings of the Seventh International Conference on Computational Structures Technology", Civil-Comp Press, Stirlingshire, UK, Paper 87, 2004. doi:10.4203/ccp.79.87
Keywords: chaos, Riemannian geometry, pendulum.
Summary
In this paper the geometrical approach is applied to describe dynamics of a
two degrees-of-freedom mechanical system. This approach has been recently widely used to study chaos in
Hamiltonian systems [1,2,3,4]. The crucial point of this method is that trajectories of a system
can be viewed as geodesics of a Riemannian manifold endowed with a metric coming from
dynamics of the analysed system. The instability of the system is linked with instability
properties of geodesics through the Jacobi-Levi-Civitta (JLC) equation, which governs the
evolution of geodesics separation. Owing to Riemann tensor occurence in the JLC equation,
instability properties are completely determined by curvature properties of the underlying
manifold. It is well-known that manifolds with negative curvature induce chaos. However, a
chaotic behaviour may also occur in systems with positive curvatures manifolds due to
curvature fluctuations along geodesics. This technique is still under development and other
classes of dynamical systems can be also analysed in this manner e.g. systems with
velocity-dependent potentials are described by Finsler geometry [4]. It is believed that geometrical
approach may provide a good explanation of the onset of chaos in Hamiltonian systems. Note
that a few manifolds can serve as a Riemannian one, for example configuration manifold with
Jacobi metric, enlarged space-time manifold with Eisenhart metric or tangent bundle of
configuration manifold with Sasaki metric. In this paper we use configuration manifold with
Jacobi metric as the Riemannian manifold, since our system is conservative. We show how
the Riemannian geometry tools govern the behavior of our two degrees-of-freedom
mechanical system with metric dependent on coordinates. The analysed system consists of
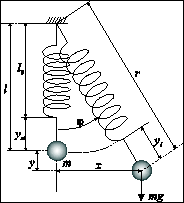
elastic swinging pendulum with nonlinear stiffness (see Figure 1).
and the relations between dimensional (see Figure 1) and non-dimensional parameters read
Since the system possesses two degrees-of-freedom, the Riemannian manifold is two-dimensional and the Riemann tensor has only one independent nonzero component. From the Jacobi-Levi-Civitta equation the Hill equation is obtained, which is further solved numerically.
The investigated system is governed by the following non-dimensional equations:
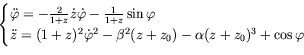 |
(30) |
and the relations between dimensional (see Figure 1) and non-dimensional parameters read
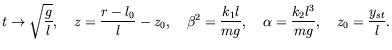 |
(31) |
Since the system possesses two degrees-of-freedom, the Riemannian manifold is two-dimensional and the Riemann tensor has only one independent nonzero component. From the Jacobi-Levi-Civitta equation the Hill equation is obtained, which is further solved numerically.
References
- 1
- L. Casetti, C. Clementi, M. Pettini: Phys. Rev. E, 54 (6), 1996. doi:10.1103/PhysRevE.54.5969
- 2
- L. Casetti, M. Pettini: Phys, Rev. E, 48 (6), 1993. doi:10.1103/PhysRevE.48.4320
- 3
- M. Cerruti-Sola, M. Pettini: Phys. Rev. E, 51 (1), 1995. doi:10.1103/PhysRevE.51.53
- 4
- M. Di Bari, P. Cipriani: Planet. Space Sci. Vol. 46 (11/12), 1998.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)