
engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE SEVENTH INTERNATIONAL CONFERENCE ON COMPUTATIONAL STRUCTURES TECHNOLOGY
Anisotropic Stress-Softening Model for Damaged Materials
+Etisalat University, United Arab Emirates
*Teesside University, United Kingdom
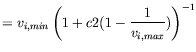 |
(16) |
where
| (17) |
and
To handle residual strain we introduce a modified strain which is a function of the principal
stretches and the unloading points. The energy function is postulated to be a function of the principal stretches
and the unloading points. A symmetric positive definte Lagrangean softening tensor
![]() which is coaxial
with the right stretch tensor is introduced in the constitutive equation.The norm of the
softening tensor is not greater than 1. The energy function
which is coaxial
with the right stretch tensor is introduced in the constitutive equation.The norm of the
softening tensor is not greater than 1. The energy function ![]() is postulated to take the form
is postulated to take the form
| (18) |
where
| (19) |
where
The Biot stress
![]()
![]() is thus given by
is thus given by
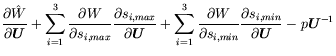 |
(20) |
Specific forms for the energy function are proposed which appear to simplify both the analysis of the three dimensional model and the evaluation of the parameter values from experimental data. Results demonstrating the effects of anisotropic stress softening are obtained for several types of homogeneous deformations. The theoretical results compare well, qualitatively and quantatively, with several experimental data exhibiting anisotropic behaviour. Numerical problems for this type of material is discussed.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)