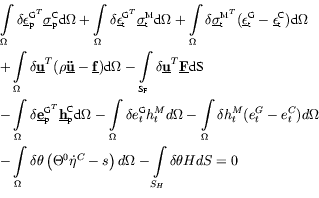Keywords: partial mixed variational principle, heat transfer, thermal stress, mixed coupled thermoelastic constitutive equations, multilayer composites.

During the last three decades a lot of research has been made on heat transfer and thermal stress analyses of layered composite structures, as attested by numerous surveys, reviews and assessments [1,2]. This can be attributed to the growing use of composite materials in high-temperature applications, even in load supporting structural components, such as in future modern aeronautic (new super liners) and aerospace (reusable launch vehicles) structures. However, most of the proposed analytical and numerical models neglect the thermoelastic dissipation in order to uncouple heat transfer and thermal stress analyses [1]. Besides, most of them are made under the steady-state assumption by considering the thermal effect only as an additional load. Generally, the heat transfer problem is first solved to get the three-dimensional (3D) distribution of the temperature, then the latter is used, via a suitable interface, as a thermal load in the structural problem.

Therefore, the solution of fully coupled heat transfer and elastic equations of motions starts to attract researchers and industrials attentions in an on-going effort to unify and integrate thermal and structural analyses. This is because, in problems where the attenuation of the dynamic disturbances resulting from the heat flow is considered, the thermoelastic dissipation is of primary interest; thus, it can not be neglected and the thermo-mechanical coupling can not be disregarded [1]. However, this requires a variational framework that can handle it suitably.

It is then the aim of this contribution to present for thermoelastic media the analogue of the Reissner's Mixed Variational Theorem (RMVT), initially developed for elastic media [3,4], by adding the transverse thermal field-temperature increment relation as a constraint via a Lagrange multiplier. The latter is shown to be the transverse (normal) heat flux, which continuity at the laminated composite interfaces can now be fulfilled in a natural way as is the case for transverse stresses in the RMVT. Hence the following new Heat Mixed Variational Theorem (HMVT) is obtained for dynamic coupled thermal stress and heat transfer analyses:

where the subscripts and stand for in-plane and transverse quantities; the superscripts , , and denote Gradient, Constitutive, Mixed and Transpose operation. The former two superscripts indicate that the relative quantities fulfil the gradient relations and the constitutive equations which have to be in a mixed form. Mixed () quantities (transverse stresses and heat flux) are to be assumed as should be done for the displacement and increment temperature

Mixed coupled thermoelastic and heat conduction constitutive equations to be used in conjunction with the HMVT, Equation (3), are shown to be:

The above HMVT is of course also valid for the quasi-static and steady-state classical cases where, as expected, thermal stress and heat transfer analyses uncouple. For the former, the HMVT reduces to the first two lines of Equation (3), whereas, for the latter, it reduces to its last two lines. They have to be used with the constitutive equations given in Equations (4) and (6), respectively.

1

Murakami, H., "Assessment of plate theories for treating the thermomechanical response of layered plates", Composites Engineering, 3, 137-149, 1993. doi:10.1016/0961-9526(93)90038-L

2

Carrera, E., "An assessment of mixed and classical theories for the thermal stress analysis of orthotropic multilayered plates", Journal of Thermal Stresses, 23, 797-831, 2000. doi:10.1080/014957300750040096

3

Reissner, E., "On a certain mixed variational theorem and a proposed application", International Journal for Numerical Methods in Engineering, 20, 1366-1368, 1984. doi:10.1002/nme.1620200714

4

Reissner, E., "On a mixed variational theorem and on shear deformable plate theory", International Journal for Numerical Methods in Engineering, 23, 193- 198, 1986. doi:10.1002/nme.1620230203

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)