Keywords: void formation, surface tension, capillary pressure, mass conservation, free boundary flow, mesolevel analysis, dual porosity.

Undesirable void formation during the injection phase of the liquid composite moulding process can be understood as a consequence of the non-uniformity of the flow front progression, caused by the dual porosity of the fibre perform. Therefore the best examination of the void formation physics can be provided by a mesolevel analysis, where the characteristic dimension is given by the fibre tow diameter in order of millimetres. In mesolevel analysis, liquid flowing along two different scales must be considered. Single scale porous media (fibre tows represented in Figure 1 by grey half-circles) and open spaces (white spaces), corresponding to different flow regimes, are presented together in the flow domain. Therefore these two flow regimes have to be coupled in one analysis. Quasi steady state assumption can be exploited in the full flow domain and explicit scheme along the time scale can be assumed.

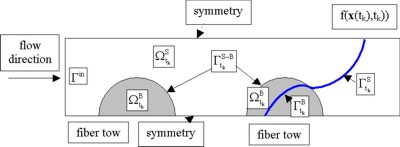
In mesolevel simulations, it is extremely important to account correctly for the surface tension effects [1,2], which can be modelled as capillary pressure applied at the flow front. However, numerical implementation of such boundary conditions leads to ill-posing of the problem, in terms of the weak classical as well as stabilized formulation. As a consequence, there is an error in mass conservation accumulated especially along the free flow front. This error can affect significantly not only the global mass conservation, but also the normal velocities at the free front and consequently distort the next front shape. Because of the explicit integration along the time scale, such errors are irreversible.

This contribution presents an appropriate technique for recalculation and correction of the normal velocities at the free front, based on the weak formulation of the problem. The methodology implemented in Darcy's region is well-known, although rarely used in real simulations. It is presented e.g. in [3]. The recalculated outlet velocities have superior convergence properties [4]. In Stoke's region the correction of the outlet velocities we are presenting have not yet been published to our knowledge. Both methodologies are implemented in the post-processing part of the existing Free Boundary Program, which can track the advancement of the resin front promoted by both hydrodynamic pressure gradient and capillary action.

Efficiency of the presented techniques is tested on simple sample problems. It can be concluded that they are very efficient. They permit calculation of frontal normal velocities with sufficient precision even for coarse meshes. Their implementation ensures better mass conservation at the global as well as the local level. It makes it possible to obtain a front shape that is not only more exact but also smoother. The computational time is reduced as coarser meshes can be used to obtain stable and accurate answers and it also allows one to step through larger time steps during the impregnation process. In order to additionally support the scheme presented for Stoke's flow, it can be proven, that in one-dimensional, even compressible case, this technique will always produce the exact analytical result, no matter what number of elements is used.

1

S.G. Advani, Z. Dimitrovová, "Role of Capillary Driven Flow in Composite Manufacturing", in "Surface and Interfacial Tension: Measurement, Theory and Applications", Hartland, S., (Editor), Surfactant Science Series, 119, Marcel Dekker, Inc., New York, Chapter 5, 263-312, 2004.

2

Z. Dimitrovová, S.G. Advani, "Mesolevel analysis of the transition region formation and evolution during the liquid composite molding process", Computers & Structures, in press, 2004. doi:10.1016/j.compstruc.2004.03.029

3

T.J.R. Hughes, G. Engel, L. Mazzei, M.G. Larson, "The continuous Galerkin method is locally conservative", Journal of Computational Physics, 163, 467-488, 2000. doi:10.1006/jcph.2000.6577

4

I. Babuška, A. Miller, "The post-processing approach in the finite element method - Part 1: Calculation of displacements, stresses and other higher derivatives of the displacements", International Journal for Numerical Methods in Engineering, 20, 1085-1109, 1984. doi:10.1002/nme.1620200610

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)