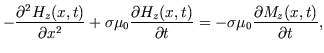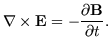(17)

which can be derived from the well known Maxwell curl equations and the constitutive relation

(18)

(19)

(20)

where the value of magnetization defined as with the scalar hysteresis operator [1].

The numerical solution of the resulting PDE is carried out by a Finite Difference Time Domain (FDTD) method, the Yee-algorithm [2], which results a two level iteration scheme. The stability of this iteration is a key point of in the solution of the problem (17), since unstable iteration does not lead to satisfactory solution. The two level iteration scheme in matrix notation is

(21)

(22)

where are band matrices with constant elements. Since Equation (22) is implicit ( ) an inner iteration has to be carried out in order to calculate from an initial estimation.

The stability analysis discussed in the paper is focusing on the inner iteration resulting from the implicit method which has to be solved in an iterative way. As the most straightforward candidate the Picard iteration method [3] is introduced for the solution of the implicit scheme.

(23)

The Picard iterative scheme 23 contains a damping constant to control the speed of the convergence and stability of the iteration. Furthermore the function in the iteration contains the nonlinear hysteresis operator with additional four parameters and the convergence of iteration is strongly depends on these parameters of the iterative map. The numerical iteration scheme of equation (23) can exhibit a wide variety of behaviors including periodic or chaotic solutions. In practical field analysis it is important to avoid situations where the iteration sticks at a certain point and fails to converge.

The main aim of the investigation is to find the reasons behind the instability of the inner iteration, and gain the stability information on the space of parameters. This goal can be approached in a way where the implicit iteration scheme is handled as a discrete dynamical system, and examination of the stability of the iteration is based on the structure of the attractor of the iterative map. The methods of stability analysis of dynamical systems can be used effectively to determine stability properties of fixed points of numerical iterations.

The examination of stability properties of the inner iteration scheme (23) proved that the reason behind the unstable behavior is a bifurcation in the attractor of the iterative map. Furthermore investigation of the parameter space of the map by the method of Lyapunov-exponents [4] proved that even if bifurcations occur and unstable parameter configurations exist in the parameter space, there are fairly large clusters of stable parameter configurations. This result encourages the calculation of calculate the damping constant of the inner iteration locally instead of applying a global stability condition to the whole map, since a local stability condition can make a more efficient use of the stability reserves of the parameter space.

1

L. A. de Almeida, G. S. Deep, A. M. N. Lima, H.Neff, "Limiting Loop Proximity Hysteresis Model", IEEE Trans.Magn, vol. 39, pp. 523-528, Jan. 2003. doi:10.1109/TMAG.2002.806344

2

A. Taflove, Computational Electrodynamics: The Finite-Difference Time-Domain Method, Artech House, Inc. 1995

3

Sheng, Song-bai; Xu, Hui-fu, "Picard Iteration for Nonsmooth Equations", Journal of Computational Mathematics, vol. 19, no. 6, pp. 583-590, Nov. 2001.

4

R. Seydel, Practical Bifurcation and Stability Analysis, Springer-Verlag, 1994

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)