Keywords: coupled vibration, thin-walled beam, shear effect.

Beams of thin-walled open cross-sections are widely used in structural design. In general, the centroid and the shear centre do not coincide; hence the flexural and the torsional vibrations are coupled. The case that the flexural vibrations in one direction are coupled with the torsional vibrations is extensively studied by many researchers. But, the case that the flexural vibrations in two mutually perpendicular directions and the torsional vibrations are all coupled is not sufficiently dealt with. Gere and Lin [1] have determined the triply coupled free vibration characteristics of uniform, open cross-section channels with simply supported ends by employing the Rayleigh - Ritz method. Yaman [2] has formulated the mathematical model by using the wave propagation approach and has presented the wave numbers for undamped and structurally damped channels. Arpaci et al. [3] have studied effect of rotary inertia on triply coupled vibrations of thin-walled beams. To the authors' knowledge, no work considering the shear effect on triply coupled vibrations of such beams appears in literature. The objective of the present study is to investigate the effect of shear on triply coupled vibrations of beams with thin-walled open cross-sections having no axis of symmetry. The effects of cross-sectional warping are also included.

Equations of Motion

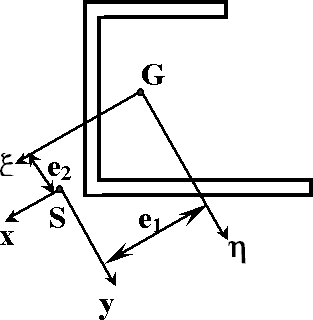
In Figure 36.1 is shown a typical cross-section of no axial symmetry where the and axes are taken through the shear centre and parallel to the principal centroidal axes and . The equations of motion may be derived by substituting inertia forces into the equations of static equilibrium as follows

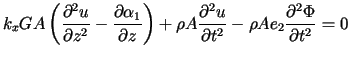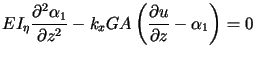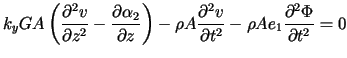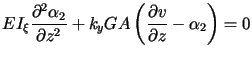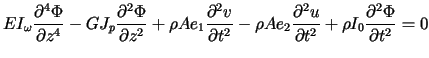where and are deflections of shear centre in and directions respectively, is angle of rotation of cross-section, and are principal centroidal moments of inertia, is warping constant, is torsion constant, and are Young's and shear moduli respectively, is polar moment of inertia about shear centre , and are co-ordinates of centroid , is cross- sectional area, is mass density, and are shear correction factors, are bending slopes and is time.

Assuming , , and five coupled equations are reduced to five independent equations by a procedure analogous to the solution of simultaneous algebraic equations where is radian frequency. The result is an ordinary differential equation of 12 th order for each function. These latter equations are solved by taking a solution in the form .

Boundary Conditions

Clamped end:
Free end:	;
Hinged end:

Numerical evaluation and Conclusions

Numerical evaluation is performed for natural frequencies and the shear effect is discussed in detail. It is shown that the accuracy of the calculations of natural frequencies is considerably disturbed in higher modes when the shear effect is not taken account of.

1

J.M. Gere, "Torsional vibrations of beam of thin-walled open section", Journal of Applied Mechanics 21, 381 � 387, 1954.

2

Y. Yaman, "Vibration of open-section channels: a coupled flexural and torsional wave analysis", Journal of Sound and Vibration, 204 (1), 131-158, 1997. doi:10.1006/jsvi.1997.0933

3

A. Arpaci, S.E. Bozdag, E. Sunbuloglu, "Triply Coupled Vibrations of Thin- Walled Open Cross-Section Beams Including Rotary Inertia Effect", Journal of Sound and Vibration, in press, 2002. doi:10.1016/S0022-460X(02)00935-5

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £125 +P&P)