Keywords: base-plates, column, connectivity, pallet racks, buckling, stability.

Storage racks fabricated from cold-formed sections are often installed on flat floors without any substantial connection between the floor and the column. Previous research into storage racks has primarily been concerned with investigations into the behaviour of the beam-to-column joints and the overall stability of frames with semi-rigid joints[1,2,3,4]. The effects of base connectivity on the overall stability of storage rack frames has received little attention. This paper investigates the failure mechanisms of columns with slenderness ratios varying from 50 to 200 both theoretically and experimentally. The model comprises a single column with one end pinned and the other end flat and which is subjected to a combined axial load and a side load applied at the middle of the column. The flat end is treated as being fixed, when it is in contact with the ground, or as an eccentrically loaded, pinned connection rotating about one edge. The model is representative of a member in the middle of a storage rack where the base-plate connecting the column to the ground is often only lightly bolted and is normally considered as pinned. A previous paper by the authors[5] investigated a slender column, using elastic stability functions[6], and concluded that such a column, resting on a flat base, was able to achieve failure loads in excess of the Euler pinned buckling failure load. Storage rack columns typically have slenderness ratios between 100 and 150 and plasticity occurs at the column-base and beam-column intersections. This paper extends the earlier work to consider the influence of plastic hinge formation on the failure mechanism of the column. 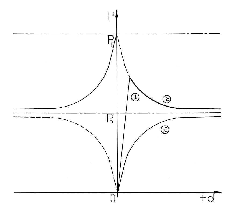The paper investigates the different failure mechanisms that can occur for a column on a flat base. The mechanisms are: failure by buckling as a column on a fixed base; failure by buckling as a column on a pinned base, including complementary paths; failures by buckling with plastic hinges at base and at the centre. In the analyses it was assumed that as the axial load increased the side load was increased in proportion. The theory shows that for a small side load that a column on a flat base behaves as if it were a column on a fixed base. The load deflection curve follows that of a fixed base. 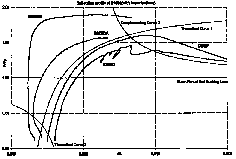This path then intersects with a complementary descending pinned-end path producing a bifurcation. (See Figure 25.1(a).) This bifurcation load is in excess of the Euler pinned buckling load. If the side load is large then the column immediately rotates about one edge of the base and cannot carry a load in excess of the Euler load. Similar phenomena occur for stockier columns where intersections with elastic rising load paths and plastic descending paths produce bifurcations. In order to verify the analysis a series of experiments was carried out. Mild steel square hollow sections of different lengths had a flat plate welded on one end and a pinned connection made at the other. Each specimen was placed in a Losenhausen column testing machine and a small axial load applied to hold the specimen into the rig. A side load was then applied at the centre of each specimen. Each specimen was then loaded to failure under displacement control. Although the theory described above was for proportional loading, a modified theory with a fixed side load was also produced. Good correlation was achieved between experiment and theory as can be seen in Figure 25.1(b). Formulae for the side loads below which loads in excess of the Euler failure load can be achieved, are derived in the paper.

1

Godley M.H.R., Beale R.G., Feng X., "Analysis and Design of down-aisle pallet rack structures", Computers & Structures, 2000, 77, 391-401. doi:10.1016/S0045-7949(00)00031-6

2

Davies J.M., "Down-aisle Stability of Rack Structures", Eleventh International Speciality Conference on Cold-Formed Steel Structures, St. Louis, MO, USA, 1992, 417-435.

3

Lewis G.M., "Stability of Rack Structures" Thin-Walled Structures, 1991,27,163-174. doi:10.1016/0263-8231(91)90062-N

4

Parsenajad S, Anderson T., "Experimental investigation of the connection behaviour in light gauge racking systems", International Conference on Steel and Aluminium Structures, ICAS 91, Singapore, 1991, 543-553.

5

Lau H.H., Godley M.H.R., Beale R.G., "The effect of column base connectivity on the carrying capacity of slender columns", 6th International Conference on Steel & Space Structures, Singapore, 1991, 397-404.

6

Horne M.R., Merchant W., "The stability of frames", Pergamon, 1965.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)