Keywords: tensile structures, membranes, cables, pseudo-stiffness.

This paper describes how a pseudo-stiffness approach may be used to simulate bending stiffness in an explicit transient dynamic analysis of cable-membrane structures. Implementaion details of the method are included with some examples. These examples demonstrate that the bending stiffness affects the simulations of these structures.

Theoretically membranes and cables have no bending stiffness. The equilibrium form of a cable and membrane structure is therefore reached when elastic forces (in plane forces for a membrane and axial forces for a cable) are in equilibrium with external forces such as gravity and the boundary condition forces. In reality all membrane and cable materials do have a certain bending stiffness. When the cable or membrane structure is discretised by a finite element mesh for loading analysis or design the forces derived from induced bending moments are only negligible when the level of discretisation is such that curvature realized between adjacent mesh elements is small.

For computational efficiency the number of elements in a simulation is to be kept as small as possible within the margins of the proposed accuracy. The high level of discretisation required to maintain negligible curvature might be too demanding for the simulation to be performed within reasonable time constraints. In this case bending stiffness must be taken into account and somehow incorporated in the simulation. The logical answer is to switch to shell elements in the simulation rather than simple elastic triangular and link elements commonly used for cable and membrane analysis. The use of more complicated elements does however increase both computation time and storage requirements. This is a sacrifice the analyst might not want to make.

In this paper a simulation of bending stiffness without major changes to the simulation kernel is presented. This implementation will be referred to as pseudo-stiffness in order to distinguish it from the traditional ways of simulating bending stiffness (e.g. using shell elements). The approach is implemented for a cable and membrane simulation kernel which uses explicit time integration of a dynamic system of masses, forces and constraints [3].

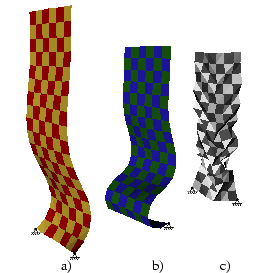
A minor out-of plane disturbance was introduced to force the cloth to buckle when all nodes are released and free-fall follows. In Figure 24.1 a `snapshot' is taken during the free-fall motion whereby the cloth is simulated for three different values of the pseudo membrane stiffness Young's modulus. Case c) is a simulation without pseudo stiffness simulation. Cases a) and b) do have pseudo stiffness enabled with

The membrane pseudo stiffness (MPS) implementation only makes significant difference in the final results when the MPS Young's modulus is several orders of magnitude larger than the overall Young's modulus.

It is obvious that the use of membrane pseudo stiffness techniques alter the dynamic characteristics of the model. Consequently the stability of the numerical integration may be affected as the eigenfrequencies of the structural model are influenced. Usually it is required to adjust the value of the timestep (unles the adaptive timestepping method is used in which case the algorithm will adjust the timestep automatically).

In some simulations finding the final equilibrium form of the membrane under specific loading conditions is not always the objective. The path the membrane follows might be more interesting than the final destination. For example, when the membrane enters into contact with other objects or makes self contact due to folds and creases, the motion of the membrane is the problem to solve.

1

N.J. Gimsing, "Cable Supported Bridges", J. Wiley and Sons, second edition edition, 1997.

2

B.H.V. Topping and P. Iványi, "Computer Aided Design of Cable-Membrane Structures", Saxe-Coburg Publications, Stirling, United Kingdom, 2002.

3

J. Muylle, B.H.V. Topping, "Contact detection and enforcement techniques for the simulation of membrane structures in motion". In "Computational Mechanics: Techniques and Developments", B.H. Topping, (Editor), pages 243-256, Civil-Comp Press, Edinburgh, U.K., 2000. doi:10.4203/ccp.66.9.4

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £122 +P&P)