Keywords: arches, elastic restraints, elasto-plastic, finite element, geometric, material, nonlinearity.

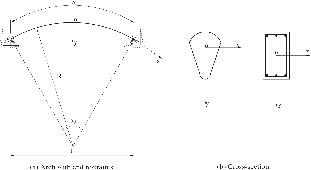
This paper presents a new curved-beam element for the in-plane geometric and material nonlinear large deformation analysis of elastically restrained arches (Figure 96.1). When the lateral and torsional deformations of an arch are fully restrained, the arch may buckle in an in-plane bifurcational mode or snap-through mode under in-plane loading. After buckling, deformations of the arch increase rapidly and become very large. Hence, in order to predict postbuckling behaviour correctly, the effects of large deformations have to be considered [1]. However, in the conventional formulations of curved-beam elements, the nonlinear strains under in-plane loading consist of nonlinear membrane strains and linear bending strains. The higher-order bending strain components produced by the higher-order curvature terms do not appear to have been considered. In addition to the higher-order curvature components due to bending, the axial deformations may affect the deformed curvatures and yield additional higher-order curvature terms. This appears to be ignored in the conventional formulations of curved-beam elements. Because of this, some significant terms in strains due to large deformations may be lost and the large postbuckling deformations cannot be predicted correctly. It is well-known that when an arch is subjected to in-plane loading, the axial compression is the major primary action in the arch. In order to produce the axial compression, the supports of arches are usually fixed or pin-ended. However, in practice, arches may be supported by elastic foundations or by other structural members which provide elastic types of restraint to the arches. The elastically restrained actions of the other elements of the structure on an arch can be replaced by equivalent springs and the arch can be considered to be restrained by the elastic springs. In many cases, by knowing the structural configuration connecting to the arch, the stiffness of the corresponding elastic springs (or spring constant) can be accurately estimated. The elastic restraints participate in the structural behaviour of the arch and may influence significantly the structural behaviour of the arch. These elastic restraints may be continuous or discrete. The curved-beam element, therefore, should consider the effects of these elastic restraints. In addition to elastic buckling and postbuckling, steel, concrete or concrete-filled tubular section arches may buckle elasto-plastically in many cases. Hence, the nonlinearity of the material needs to be included in the curved-beam element as well.

A curved-beam element is developed in this paper based on an accurate rotation matrix that satisfies the orthogonality and unimodular conditions. Therefore, the higher order terms of the deformed curvatures in strains and the effects of the axial deformations on the deformed curvatures are retained and thus the large deformations can be predicted accurately by the element. At the same time, the membrane locking problem that occurs in a number of curved-beam elements is naturally avoided because the same order interpolation polynomials can be used for both radial and axial deformations. In addition, the curved beam element includes the effects of the elastic restraints on the structural behaviour of arches. Furthermore, material nonlinearity in the elastic and elasto-plastic ranges are considered in the curved-beam element as well.

Comparisons of results of the finite element model with the analytical closed form solutions [2] for buckling and postbuckling of elastically restrained arches, and with the test results [3] demonstrate that the curved beam element provides a good prediction accuracy for nonlinear analysis.

1

Pi, Y.-L. and Trahair, N.S. "Non-linear buckling and postbuckling of elastic arches", Engineering Structures 20(7), 571-579, 1998. doi:10.1016/S0141-0296(97)00067-9

2

Pi, Y.-L., Bradford, M.A., and Tin-Loi, F. "In-plane stability of elastically restrained arches", Research Report, School of Civil and Environmental Engineering, The University of New South Wales Structures, Sydney, Australia, 2005.

3

Wang, T., Bradford, M.A. and Gilbert, R.I. "Short-term experimental study of a shallow reinforced concrete parabolic arch", Australian Journal of Structural Engineering, 6(1), 53-60, 2005. doi:10.1002/cnm.753

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)