engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE TENTH INTERNATIONAL CONFERENCE ON CIVIL, STRUCTURAL AND ENVIRONMENTAL ENGINEERING COMPUTING
Topological and Graph Products: Eigenproblems for Optimal Structural Analysis
Iran University of Science and Technology, Narmak, Tehran, Iran
Consider a planar grid ![]() produced as the Cartesian product of two paths
produced as the Cartesian product of two paths
![]() ,
with
,
with ![]() . The grid is bent and the two edges along
. The grid is bent and the two edges along ![]() are connected to each
other by
are connected to each
other by ![]() disjoint members, producing a cylindrical-shaped grid
disjoint members, producing a cylindrical-shaped grid ![]() . Naturally,
the number of nodes of
. Naturally,
the number of nodes of ![]() and
and ![]() are identical, and
are identical, and ![]() has
has ![]() members more than
members more than
![]() . Similarly, a torus-shaped grid
. Similarly, a torus-shaped grid ![]() is formed from
is formed from ![]() by the addition of
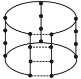
by the addition of ![]() members to its free edges, as shownm in Figure 95.1
members to its free edges, as shownm in Figure 95.1
In this paper it is proved that
![]() . Thus, without considering specific
values for
. Thus, without considering specific
values for ![]() and
and ![]() , and only by assuming
, and only by assuming ![]() , it is concluded that the second
eigenvalue of
, it is concluded that the second
eigenvalue of ![]() is the same as the third eignvalue of
is the same as the third eignvalue of ![]() .
.
As an example, for ![]() and
and ![]() , we have
, we have
| For |
||
| For |
Similarly, it can be proved that the third eigenvalue
![]() and the second
eigenvalue
and the second
eigenvalue
![]() are identical; i.e.
are identical; i.e.
![]() .
.
For direct and strong Cartesian products the same results are applicable, and
![]() and
and
![]() .
.
As an example, for ![]() and
and ![]() , the following results can be observed:
, the following results can be observed:
| For a direct product: |
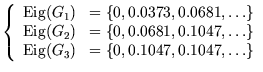 |
|
| For a strong Cartesian product: |
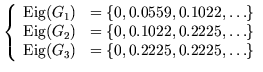 |
The eigenvalues of the adjacency and Laplacian matrices of three different graph products, provide an efficient approach for calculating the eigenvalues of adjacency and Laplacian matrices of weighted and non-weighted graphs. The eigensolution of graphs has many applications in computational mechanics. Examples of such applications are nodal and element ordering for bandwidth, profile and frontwidth optimization, graph partitioning, and subdomaining of finite element models [1,2]. The present forms are also effective tools for calculating eigenvalues and eigenvectors of matrices arising form numerical methods for differential equations applied to structural mechanics problems.
- 1
- Kaveh A. "Structural Mechanics: Graph and Matrix Methods", Research Studies Press, Exeter, U.K., 3rd edition, 2004.
- 2
- Kaveh A. "Optimal Structural Analysis", Research Studies Press, Somerset, U.K., 1997.
- 3
- Kaveh, A. and Rahami, H., "A unified method for eigendecomposition of graph products", Communications in Numerical Methods in Engineering, 2005, in press. doi:10.1002/cnm.753
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £135 +P&P)