Keywords: contact, friction, modelling, numerical methods.

Friction is a natural occurrence that affects almost all objects in motion. The miracle of fire by friction was perhaps the first manifestation of friction for our ancestors, ten thousand years ago. In antiquity people used grease in order to move stones on inclined planes. Since then extensive research has attempted to develop models that accurately predict friction behaviour. This paper outlines modelling and computational methods for studying contact between deformable solids. 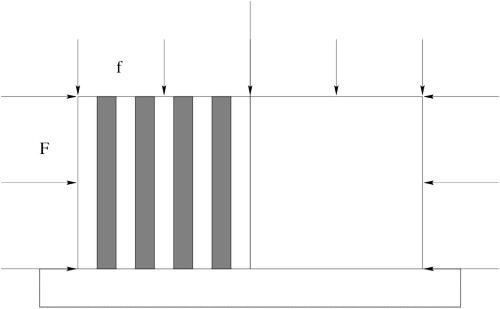In the first part of the paper some contact laws are presented. We focus on Signorini's law and the semi-empirical Coulomb law, which are convenient for a large class of structures. In order to solve the problem, two families of algorithms are presented. The first one is based on a fixed point algorithm on the implicit friction term [1]. At each iteration of the fixed point algorithm, we have to solve an optimization problem with constraints. The problem is not differentiable and is classically solved by relaxation procedures. This algorithm has been used by the author and his collaborators for the analysis of a complex assembly in reactor technology [2] and for the analysis of coupling sleeves in shape memory alloys [3]. The numerical results have been compared with experimental data and a validation of the model has been obtained for the first application. This method is very simple to implement and to couple with complex behaviours. It is a robust method and the convergence does not depend much on the friction coefficient. The second algorithm is based on a mixed formulation and leads to nonlinear and non-differentiable problems. These problems are solved by a generalised Newton method. The tangent matrix of the system is non-symmetric, non-positive definite, ill-conditioned and with zeros on the diagonal. Consequently, it is necessary to design appropriate preconditioners [4]. Industrial problems such a system of rolling shutters and a leaf spring-dashpot suspension system have been analysed in earlier papers [5]. 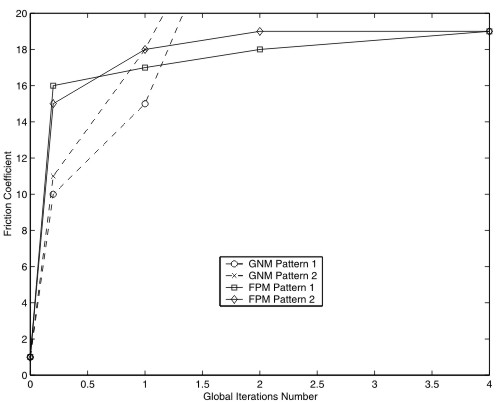The last part of the paper is devoted to a comparison between the methods presented above. The academic example of a composite long bar in contact with a rigid obstacle is treated. This problem has the advantage of presenting complex contact zones and very ill-conditioned stiffness matrices. An analysis of the efficiency and robustness of the two algorithms is given.

1

M. Raous, P. Chabrand, and F. Lebon. "Numerical methods for solving unilateral contact problem with friction", Journal of Theoretical and Applied Mechanics, 7:111-128, 1988.

2

F. Lebon and M. Raous. "Friction modelling of a bolted junction under internal pressure loading", Computers and Structures, 43:925-933, 1992. doi:10.1016/0045-7949(92)90306-K

3

S. Pagano, P. Alart, and F. Lebon. "Un algorithme de décomposition convexe pour l'étude de structures en alliage à mémoire de forme. Application aux manchons de raccordement", European Journal of Finite Elements, 7:365-400, 1998.

4

P. Alart and F. Lebon. "Solution of frictional contact problems using ILU and coarse/fine preconditioners", Computational Mechanics, 16:98-105, 1995. doi:10.1007/s004660050053

5

K. Ach, P. Alart, M. Barboteu, F. Lebon, and B. Mbodji. "Parallel frictional contact algorithms and industrial applications", Computer Methods in Applied Mechanics and Engineering, 177:169-181, 1999. doi:10.1016/S0045-7825(98)00379-X

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)