Keywords: composite shells, stability, buckling, robust design.

Thin-walled shell structures like circular cylindrical shells are prone to buckling. Imperfections which are defined as deviations from perfect shape and perfect loading distributions can reduce the buckling load drastically compared to that of the perfect shell. Design criteria monographs like NASA-SP 8007 recommend that the buckling load of the perfect shell shall be reduced by using a knockdown factor. The existing knockdown factors are very conservative and do not account for the structural behaviour of composite materials. To determine an improved knockdown factor several authors consider the realistic shape of the shell in a numerical simulation using probabilistic methods. For this probabilistic approach a large number of test data is needed which is often not available. Motivated by this lack of data a new deterministic approach is presented for determining the lower bound of the buckling load of thin-walled cylindrical composite shells. It is derived from phenomenological test data.

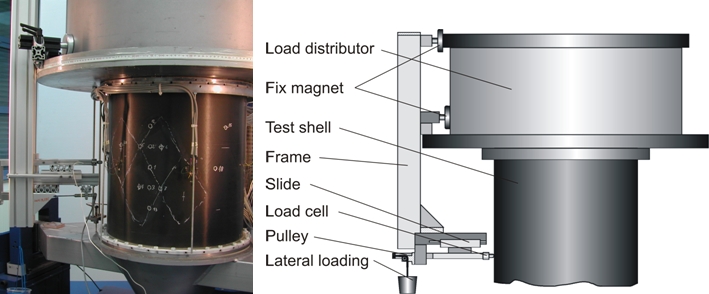
Previous investigations have shown that a single buckle is a realistic, worst case and stimulating geometric imperfection of thin-walled cylindrical shells [1,2,3]. The single pre-buckle is induced by a perturbation rig 1. The influence of a radial perturbation load on the structural behaviour is investigated by applying loads of different magnitudes and at different positions along the circumference. 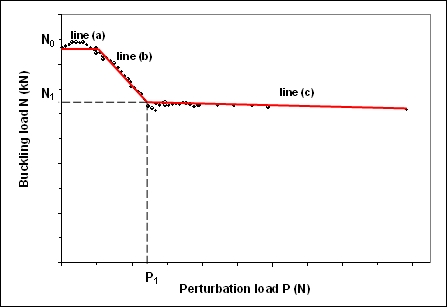The results of one perturbation position are shown in Figure 2. Each dot marks one test and shows the buckling load as function of the perturbation load . The run of the curve is shown by three lines (Figure 2). For perturbation loads larger than the reduction of the buckling load is quite small. This means that the perturbation load has to be increased very strongly in order to reduce the buckling load any further. For perturbation loads single buckles are clearly visible, can be detected by inspection and are therefore assumed to be unrealistic. The buckling load at the intersection point of lines (a) and (b) is defined to be the new lower limit for the buckling load of realistic imperfect composite shells.

Based on the test results the numerical analysis is validated. The results of the tests and the numerical analysis are compared to the values of the NASA-SP 8007. The new approach leads to a much less conservative, but also safe, design. The possibilities for practical use are shown using a design example.

1

M. Deml, W. Wunderlich, "Direct evaluation of the `worst' imperfection shape in shell buckling", Computer Methods in Applied Mechanics and Engineering, 149(1-4), 201-222, 1997. doi:10.1016/S0045-7825(97)00055-8

2

T. Winterstetter, H. Schmidt, "Stability of circular cylindrical steel shells under combined loading", Thin-Walled Structures, 40, 893-909, 2002. doi:10.1016/S0263-8231(02)00006-X

3

C. Hühne, R. Rolfes, H. Klein and J. Tessmer, "New Approach for Robust Design of Composite Cylindrical Shells under Axial Compression", European Conference on Spacecraft Structures, Materials and Mechanical Testing, ESA/ESTEC, Nordwijk, The Netherlands, 2005.

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)