Keywords: fluid-structure interaction, coupled problem, non-conforming meshes, iterative method, sub-structuring, parallel computing.

Many areas of engineering and physics require powerful algorithms to solve huge problems. Sub-structuring methods and preconditioning techniques based on domain decomposition [1,4,5,7] are very efficient for computing the solution of large scale problems in parallel. These methods mainly consist of splitting the global domain into several sub-domains and computing the solution on the global domain through the solution of the problems associated with each sub-domain. Major research has been done on these techniques and methods during the last fifteen years. Novel algorithms, new preconditioners and new fields of application have been successfully investigated. One of the current research challenges in the field when handling real-life engineering problems consists of solving coupled problems.

In this paper a general methodology to solve coupled fluid-structure problems is presented. The proposed coupling is usually called 'weak-coupling' in the literature because the equations are coupled through the boundary conditions and the coupling occurs on the right hand side only. The proposed method is based on a sub-structuring method, where each sub-domain consists of a single-physics problem. Coupling between the sub-domains is insured through coupled quantities.

A locally optimal preconditioning technique based on the exact solution of fluid and structure, independent subproblems, is proposed here. A key property of the iterative solution of the preconditioned coupled problem is that only the restrictions on the interface of the vectors built at each iteration need to be stored, making the implementation of the robust Krylov method, with full orthogonalization, inexpensive. In addition, at each iteration, each independent (single-physics) subproblem is solved in parallel.

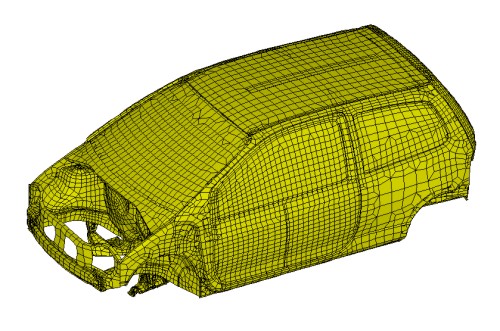
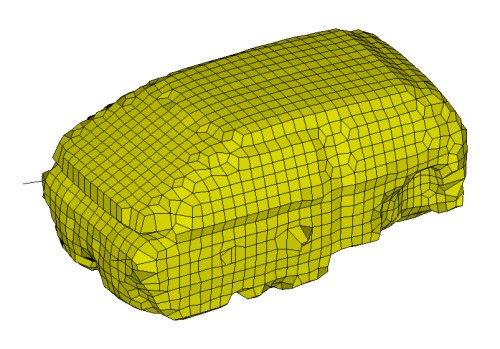
When dealing with coupled fluid-structure interaction problems, one major difficulty lies in the non-matching grids between the mesh of the fluid and the mesh of the structure. In Figure 1 is an example of non-matching grids between the structural mesh of a car body, and the associated acoustic mesh of a car compartment, which clearly outlines this difficulty.

Contrary to the MpCCI [3] software based on a mortar finite element discretization on the fluid-structure interface, this paper proposes to integrate the coupled quantities on a set of quadrature points. This approach only involves the computation of nodal values and interpolation at given Gauss points, which allows any -refinement.

In the numerical experiments the evaluation of the frequency response function of a driver's ear, due to vibration of a car body, is investigated. This example is representative of a wider class of problems where one tries to evaluate the acoustic response within a cavity as induced by some vibrations. The single-physics problems are solved respectively with MSC [2] for the vibro-elasticity analysis and with SYSNOISE [6] for the acoustic analysis. An additional coupling module is used to manage coupling between the single-physics problems.

1

F. Magoulès and T. Kako (eds.). "Domain Decomposition Methods: Theory and Applications". Gakuto International Series, Mathematical Science and Applications, Gakkotosho Tokyo Japan, vol.25, 2006.

2

MD Nastran. "Multidiscipline simulation system for advanced engineering analysis". www.mscsoftware.com, 2006.

3

MpCCI 3.0. "Multidisciplinary simulations through code coupling". Fraunhofer-Institute SCAI, www.scai.fraunhofer.de, 2006.

4

A. Quarteroni and A. Valli. "Domain Decomposition Methods for Partial Differential Equations". Oxford University Press, Oxford, 1999.

5

B. Smith, P. Bjorstad and W. Gropp. "Domain Decomposition: Parallel Multilevel Methods for Elliptic Partial Differential Equations". Cambridge University Press, 1996.

6

SYSNOISE Rev. 5.6. "A software tool for vibro-acoustic simulation". LMS International, Interleuvenlaan 70, 3001 Leuven, Belgium.

7

A. Toselli and O.B. Widlund. "Domain Decomposition Methods: Algorithms and Theory". Springer Series in Computational Mathematics, vol.34, 2004.

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)