Keywords: elastohydrodynamic lubrication, finite elements, discontinuous Galerkin, mesh adaptivity.

Friction is an essential force that occurs in all aspects of our everyday life, allowing us to walk or making cars both run and stop for example. However, sometimes friction is not welcome: it can cause power loss in engines or reduce the lifetime of contacting elements (due to wear). In these situations, it is desirable that frictional forces should be minimised. The most common way to reduce friction and prevent wear is through lubrication, where lubricants are used to separate contacting surfaces, allowing the efficiency of components to be significantly enhanced and the lifetime of machine elements to be dramatically extended. It is not surpising therefore that understanding lubricant behaviour is a long-standing problem of interest to researchers. In many cases, the film thickness is determined exclusively by the shapes of the contacting surfaces. This situation is called hydrodynamic lubrication. However, when the pressure is sufficiently high, compared to the stiffness of the running surfaces, the elastic deformation of the contacting surfaces cannot be ignored, and this can heavily affect the shape of the lubricant film. The lubrication of such, more complicated, situations is known as elastohydrodynamic lubrication (EHL): the topic of this paper.

The EHL problem is not only characterised by the interaction between the film thickness and the elastic deformation. At such high pressures, the lubricant viscosity also depends heavily on pressure and the lubricant is compressible. A very interesting feature of the flow is a steep pressure spike that appears in the outlet region at high loads. The precise loading configuration affects both the shape and the position of the spike which can be very sharp indeed, although it is always smooth. Another important characteristic element of EHL is the outlet free boundary (or cavitation position) where the pressure of the lubricant becomes equal to the vapour pressure (conventionally taken to be zero). All of these features significantly increase the complexity of EHL problems compared to hydrodynamic lubrication problems.

In this paper we propose use of the discontinuous Galerkin (DG) method for the solution of both steady-state and time-dependent EHL problems. Originally the DG method was introduced for purely hyperbolic problems however in [2] a new variant was introduced that extended DG in a natural manner to second order convection-diffusion problems. Over each element boundary, both solution values and fluxes may be discontinuous: with continuity across inter-element boundaries, and the boundary conditions, only imposed weakly. For diffusion problems this method may be proved to be highly accurate as the degree of the approximating polynomials is increased. Furthermore, in convection-dominated cases, no artificial diffusion is required to improve the stability. Hence this is a high-order scheme which is applicable to both convection-dominated and diffusion-dominated equations. This property makes it an ideal candidate to be applied to EHL problems which can be both convection- and diffusion-dominated in different regions of the domain.

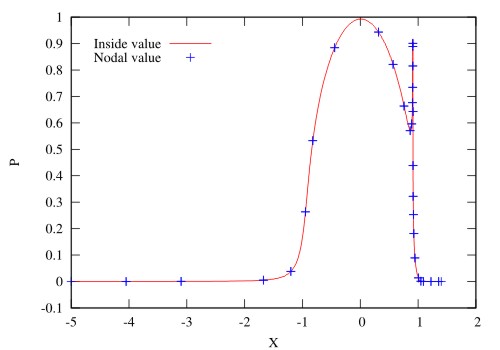
A further attraction of the DG method is the ease with which mesh adaptivity may be implemented. Since the solution is discontinuous over element interfaces, adaptivity can be easily performed without the restrictions imposed by the continuity requirements of the continuous finite element method. Numerous results will be presented in order to demonstrate the power of the adaptive DG method. For example, Figure 1 shows a pressure profile computed for a typical highly loaded case using elements of degree 12. Note the sharp pressure spike that is a typical feature of such solutions.

1

Lu H., Berzins M., Goodyer C.E. and Jimack P.K. High order discontinuous Galerkin method for elastohydrodynamic lubrication line contact problems. Comm. Numer. Meth. Engng., 21:643-650, 2005. doi:10.1002/cnm.781

2

I. Oden, J.T. Babuska and C.E. Baumann. A discontinuous hp finite element method for diffusion problems. J. Comput. Phys., 146:495-519, 1998. doi:10.1006/jcph.1998.6032

purchase the full-text of this chapter (price £20)

go to the previous chapter
go to the next chapter
return to the table of contents
return to the book description
purchase this book (price £90 +P&P)