Keywords: hybrid systems, fuzzy sets, fuzzy numbers, fuzzy differential equations, Euler method, Runge-Kutta method.

The study of differential equations through the interaction of both continuous valued and discrete valued variables leads to the study of hybrid systems. Hybrid systems contain a mixture of logic, discrete value dynamics and continuous variable dynamics. The differential equations containing fuzzy valued functions and the interaction with a discrete time controller can be named as hybrid fuzzy differential equations.

In [1,2], using the idea of perturbing Lyapunov-like functions, we developed nonuniform stability criteria for solutions of hybrid fuzzy differential systems. For this purpose, we developed comparison theorems in terms of a Lyapunov-like function employing the theory of fuzzy differential inequalities. In these articles various stability concepts are developed to understand the solution properties of hybrid fuzzy systems.

The development of nonuniform boundedness criteria for the solution of hybrid fuzzy differential equations under weaker assumptions using the idea of the perturbation of a Lyapunov-like function can be found in reference [3].

Hybrid fuzzy systems on time scales is an another important concept of research interest. In [4] we developed a comparison principle and practical stability results for hybrid fuzzy systems on a time scale. The notion of practical stability is more useful when the desired system may be mathematically unstable and yet the system may oscillate sufficiently near the state that its performance is acceptable. For a basic discussion on fuzzy-valued functions and detailed discussion of fuzzy differential equations we refer to [5,6].

In recent years it has been established that numerical solutions for fuzzy differential equations convey more understanding of the solution process compared to the numerical solutions of differential equations. Numerical methods for fuzzy differential equations are developed in [7,8,9,10]. It is very important now to analyze numerically the differential systems containing fuzzy valued functions and their interaction with a discrete time controller. For numerical treatment of hybrid fuzzy differential equations we refer to [11].

In this article we consider the hybrid fuzzy differential systems

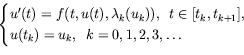where u, f, , are fuzzy valued functions. We assume the required conditions for the existence and uniqueness of solutions.

In this paper we apply the well known numerical methods, namely, the Euler method and the Runge-Kutta method to hybrid fuzzy differential equations. We list some preliminaries of fuzzy valued functions and present in detail the Euler and Runge-Kutta methods for hybrid fuzzy differential equations. In addition we discuss the rate of convergence and order of convergence of the numerical methods. To illustrate the theory we present several numerical examples of hybrid fuzzy systems.

1

M. Sambandham, "Perturbed Lyapunov-like functions and hybrid fuzzy differential equations", International J. Hybrid Sys., 2, 23-34, 2002.

2

M. Sambandham, "Method of Vector Lyapunov-Like Functions and Hybrid Fuzzy Differential Systems", Dynamic Systems and Applications. 13 (2004) 581- 591.

3

M. Sambandham, "Boundedness Properties of Hybrid Fuzzy Differential Equations", Dynamic Systems and Applications 15 (2006) 149-156.

4

M. Sambandham, "Hybrid Fuzzy Systems on Time Scales", Dynamic Systems and Applications. 12 (2003) 217-227.

5

V. Lakshmikantham, X.Z. Liu, "Impulsive hybrid systems and stability theory", Intern. J. Nonl. Diff. Eqns., 5, 9-17, 1999.

6

V. Lakshmikantham, R.N. Mohapatra, "Theory of Fuzzy Differential Equations and Inclusions", Taylor and Francis, United Kingdom, 2003.

7

M. Ma, M. Friedman, A. Kandel, "Numerical solutions of fuzzy differential equations", Fuzzy Sets and Systems, 105, 133-138, 1999. doi:10.1016/S0165-0114(97)00233-9

8

S. Abbasbandy, T. Allah Viranloo, "Numerical solution of fuzzy differential equations by Taylor method", J. of Computational Methods in Applied Mathematics, 2, 113-124, 2002.

9

S. Abbasbandy, T. Allah Viranloo, "Numerical solution of fuzzy differential equation", Mathematical and Computational Applications, 7, 41-52, 2002.

10

S. Abbasbandy, T. Allah Viranloo, "Numerical solution of fuzzy differential equation by Runge-Kutta method", Nonlinear Studies, 11, 117-129, 2004.

11

S. Pederson, M. Sambandham, "Numerical solution to hybrid fuzzy systems", submitted for publication. doi:10.1016/j.mcm.2006.09.014

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)