Keywords: error estimation, stress recovery, superconvergent patch recovery, generalised stress intensity factor, equivalent domain integral, finite element method, singular stress fields.

When applied to smooth solution problems, recovery-type error estimators, especially those based on the use of the superconvergent patch recovery (SPR) technique [1], have been shown to provide very accurate results. However, the efficiency of the error estimators decreases in singular problems due to their special nature.

In this paper, a new recovery-type error estimator for singular problems in linear elasticity, called the SPR-C-GSIF technique, has been developed. The idea behind the new recovery technique is to obtain the recovered stresses as the contribution of a singular recovered stress field and a smooth recovered stress field . The recovered singular stress field is reconstructed once the generalised stress intensity factor K (GSIF) is extracted from the standard finite element solution. The value of K, which characterizes the singular field, is then substituted into the singular analytical expressions for the stresses to have a better estimate of the singular part of the stress field. For the smooth recovered stress field, an enhanced SPR technique [2] which ensures the exact satisfaction of the equilibrium and compatibility equations of the recovered stresses in the patch is used. The stresses are directly evaluated at the integration points using a 'conjoint polynomial' enhancement to account for the different values of stresses obtained at each integration point from different patches.

In order to obtain an accurate estimation of the GSIF, a domain integral approach has been used [3]. The use of domain integrals for characterizing elastic singular problems is very efficient, accurate and easy to implement as a post-processing part of a finite element analysis.

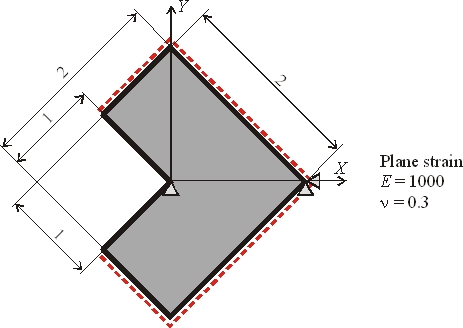
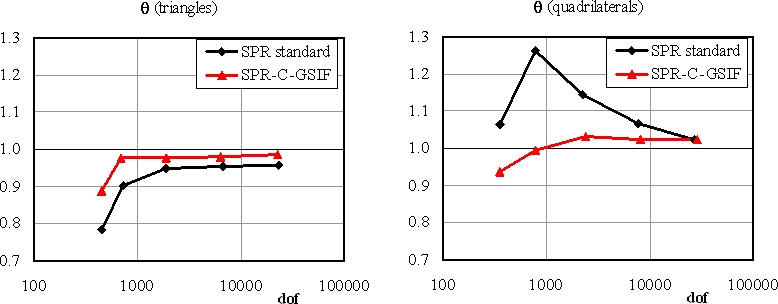
The test problem used in the numerical examples is a portion of an infinite L-shaped domain which has been loaded with pure mode I stresses, see Figure 1. Since the effectivity index is a measure of the ratio of the estimated error to the exact error , Figure 2 compares the global effectivity indices obtained using the proposed method with the results obtained with the standard SPR technique. A clear improvement can be observed. It has also been checked that the improvement is remarkable at the local level.

1

O.C. Zienkiewicz, J.Z. Zhu, "The Superconvergent Patch Recovery and a-Posteriori Error Estimates. Part I: The Recovery Technique", International Journal for Numerical Methods in Engineering, 33, 1331-1364, 1992. doi:10.1002/nme.1620330702

2

J.J. Ródenas, M. Tur, F.J. Fuenmayor, A. Vercher, "Improvement of the superconvergent patch recovery technique by the use of constraint equations: the SPR-C technique", Submitted to International Journal for Numerical Methods in Engineering, 2005. doi:10.1002/nme.1903

3

B.A. Szabó, I. Babuška, "Finite Element Analysis", John Wiley & Sons, Inc., New York, 1991.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)