Keywords: isomorphism of Markov chain, probabilistic regulatory networks, Boolean network, transition matrix, category, dynamical systems.

We can understand the complex interactions of genes using simplified models, such as discrete or continuous models of genes. Developing computational tools permits description of gene functions and understanding the mechanism of regulation [3]. We focus our attention in the discrete structure of genetic regulatory networks instead of continuous models. The probabilistic gene regulatory network (PRN) is a natural generalization of the probabilistic boolean network (PBN) model introduced in [4,1]. This model has n functions defined over a finite set X to itself, with probabilities assigned to these functions. We present here the ideas of -similar networks, and isomorphism of Markov Chains, using the concept of -homomorphisms, where , is a distance between the probabilities. A probabilistic regulatory network (PRN) [1] is a triple where X is a finite set and is a set of functions from X into itself, with a list of selection probabilities, where . The state space is a digraph, whose vertices are the elements of X, and if , there is an arrow going from u to v, and the probability is assigned to this arrow.

If is a set of selection probabilities we denote by the characteristic function over , such that , if and . Let and be two PRN. A map is an -homomorphism from to , if for a fixed real number , and for all there exists a , such that for all u, v in , and If is a bijective map, and , for all , , u, and v in ; then is an isomorphism. If and are bijective -homomorphisms, then the transition matrices and satisfy the condition max , for all ; u, v, in , where , and . This property determines a correspondence between the Markov chains of these two networks. Here, we introduce the concept of two similar time discrete Markov chains (TDMC). Two TDMC of the same size : , and , are -similar or -isomorphic if a exists that is small enough, such that satisfies that for all m, where is the characteristic function.

For example: suppose we have two genes with two values that we denote as usual , that is this PRN is a very simple PBN. The set of boolean functions F is the following: and the probabilities are . In Figure 1, the PBN , its state space, dependency graph, and transition matrix, are shown.

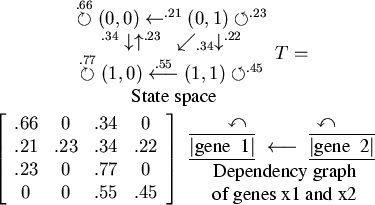A mathematical method is constructed here given the dependency graph of a set of genes. These genes could have either two, or three values. The model that we obtain gives the information about the subnetworks, the possible projections, and the fixed points. We present here a methodology for construct discrete networks using the dependency graph and a time series data. For genes with more than two states, we assign three possible values , and using the algorithm introduced in [2] we calculate the model PRN.

1

M. A. Aviñó, "Homomorphisms of Probabilistic Gene Regulatory Networks", Proceedings of GENSIPS 2006.

2

M. A. Aviñó, E. Green, and O. Moreno, "Applications of Finite Fields to Dynamical Systems and Reverse Engineering Problems", Proceedings of ACM Symposium on Applied Computing, 2004. doi:10.1145/967900.967939

3

E. R. Dougherty, A. Datta, and C. Sima, "Developing therapeutic and diagnostic tools", Gen.Sig. Proc., IEEE Signal Processing Magazine, 46-68, Nov. 2005.

4

I. Shmulevich, E. R. Dougherty, and W. Zhang, "From Boolean to probabilistic Boolean networks as models of genetic regulatory networks", Proc. of the IEEE. 90(11): 1778-1792, 2001. doi:10.1109/JPROC.2002.804686

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)