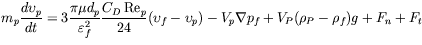engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Computational Simulation of the Influence of Moving Solid Particles on Species Diffusion and Chemical Reactions
1Centre for Material and Fibre Innovation, Deakin University, Geelong, Australia
2Centre for Advanced Manufacturing and Research, University of South Australia, Mawson Lakes, Australia
A standard
![]() turbulent model is used for the continuous gas phase. The standard
momentum, energy and species diffusion equations are modified by considering the
interaction of the solid particles and the continuous gas phase. The mass,
momentum, energy, and species conservations of a continuous fluid phase are
described by the following generalized equation:
turbulent model is used for the continuous gas phase. The standard
momentum, energy and species diffusion equations are modified by considering the
interaction of the solid particles and the continuous gas phase. The mass,
momentum, energy, and species conservations of a continuous fluid phase are
described by the following generalized equation:
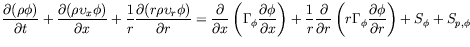 |
(103) |
where the general variable
Both the finite rate model (FRM) and the eddy dissipation model (EDM) are employed in the present work to calculate the overall chemical reaction rate. The EDM describes the effect of turbulence on the reaction rate. The eddy dissipation reaction rates are calculated based on the work of Magnussen and Hjertager [1]. The FRM describes the effect of temperature and concentration of the species on the reaction rate. The rate of reaction for any reactant is assumed to be given by the Arrhenius expression. The lower rate, out of the eddy dissipation rates and the chemical kinetics rate, is the limiting rate of reaction and is used for the calculations.
The particle phase is simulated by the discrete element method (DEM) [2,3].
The motion of every individual particle in the system is described by the Newtonian
equation of motion, equation (104). The left term in equation (104) is the change of
particle momentum and the right terms are the forces acting on the particle. They are
the drag force (term 1), the force (term 2) due to the pressure gradient in the gas, the
buoyancy (term 3), and the normal and the tangential particle-particle contact
interaction forces (![]() and
and ![]() ), respectively.
), respectively.
In the simulation, the governing equations are solved sequentially. Because the equations are non-linear and coupled, several iterations of the solution loop were performed before a convergence is achieved. The simulation results show that the inert particles change the pattern of gas flow and cause the gas circumfluence in the reaction zone. This enhances the diffusion of the reactants and products and increases the chemical reaction rates. As heat carriers, the hot particles heated in the high temperature region move to the reactor bottom and transfer their heat to the cold methane and air. As the results, the propagation of the reactions starting from the reactor wall is accelerated and, or the reactants are heated to the activation temperature and then the reactions are ignited. The charge of solid particles in a reactor also makes the reactants and products distribute uniformly in the reactor.
- 1
- B.F. Magnussen and B.H. Hjertager, "On mathematical models of turbulent combustion with special emphasis on soot formation and combustion", in "Proc. 16th Symp. (Int'l.) on Combustion", Cambridge, MA, The Combustion Institute, 1976. doi:10.1016/S0082-0784(77)80366-4
- 2
- Y. Tsuji, T. Kawaguchi, and T. Tanaka, "Discrete particle simulation of a fluidized bed", Powder Technology, 77, 79, 1993. doi:10.1016/0032-5910(93)85010-7
- 3
- M.J. Rhodes, et al., "Study of mixing in gas-fluidized beds using a DEM model", Chemical Engineering Science, 56(8), 2859-2866, 2001. doi:10.1016/S0009-2509(00)00524-8
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)