Computational Technology Resources - CCP

Keywords: finite element modelling, hysteresis, magnetic force.

Summary

In this paper a one-dimensional computational problem has been introduced with nonlinear hysteresis. The materials have been modeled with the well-known

hysteresis characteristic between the magnetic field intensity H and the magnetization M. In the paper a finite element (FE) method is combined with modeling of ferromagnetic material. Post processing of the nonlinear field problem yields the investigation of magnetic forces between the plates. The final purpose is to study the energy losses and the vibration generated sound due to the magnetic forces.

The goal of this paper is to derive the magnetic field intensity H inside two infinite large plates with d=7mm and compute the magnetic forces between the plates.

The governing equations of the FE model can be described by Maxwell's equations

(97)

and the following equation yielding

(98)

Reducing for the one-dimensional problem in direction z

(99)

For the nonlinear material modeling the hysteresis characteristic with function is described as

(100)

where H₀ the magnetic field intensity at

and

is the value of the magnetization in saturation. For linear material modeling the relationship

has been used.

The model has been applied to a one-dimension problem in the z direction with sinusoidal excitation at the boundaries. The Dirichlet boundary conditions are defined as with an excitation frequency of f=500Hz.

The magnetic force along z direction can be calculated by the following equation

(101)

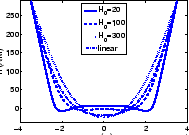
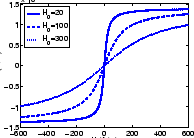
where B_y is the variation of the magnetic flux density induced in the material by the magnetic field along the z direction. Different numerical techniques have been considered for the time step process. The solution is calculated by combining a Comsol FE solver for the time independent, stationary nonlinear problem and a fixed-point iteration for every time step. In Figure 1 the H field deformation due to the characteristic between H and M can be seen, where different H₀ values occurs different diffusion behavior.

Figure 1: The magnetic field intensity in one-dimension with nonlinear and linear material modeling at *t=5T/4*. The nonlinear hysteresis model has been defined by the *tan^-1* function.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)