
Computational & Technology Resources
an online resource for computational,
engineering & technology publications
engineering & technology publications
Civil-Comp Proceedings
ISSN 1759-3433
ISSN 1759-3433
CCP: 84
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
Edited by: B.H.V. Topping, G. Montero and R. Montenegro
Paper 183
Stochastic Stability of Linear and Nonlinear Fluid Structure Coupled System with Non-Gaussian Multiplicative Noise
F. Poirion1, B. Puig2 and I. Zentner3
1French Aeronautics and Space Research Center, Chatillon, France
2Mathematical Laboratory, University of Pau, France
3France Electricity, EDF, Clamart, France
Full Bibliographic Reference for this paper
F. Poirion, B. Puig, I. Zentner, "Stochastic Stability of Linear and Nonlinear Fluid Structure Coupled System with Non-Gaussian Multiplicative Noise", in B.H.V. Topping, G. Montero, R. Montenegro, (Editors), "Proceedings of the Fifth International Conference on Engineering Computational Technology", Civil-Comp Press, Stirlingshire, UK, Paper 183, 2006. doi:10.4203/ccp.84.183
Keywords: aeroelasticity, non-Gaussian, random dynamical system, stability.
Summary
In a previous paper [2] the stability of fluid-structure coupled systems in turbulent flow has
been investigated under the assumption that turbulence was introduced as a stationnary
Gaussian random process. The coupled system behaviour will be described using the random
dynamical system context [3].
It is well known that the stability of linear random dynamical systems can be examined by
the means of Lyapounov exponents. This approach can be extended to the case of nonlinear systems
by linearising in the vicinity of fixed points. The use of Lyapounov exponents and more generally of
the Oseledets' theorem necessitates rather restricting assumptions for the random noise which must be
modelled as a regular diffusion. That explains why, in practice, only Gaussian multiplicative noises
are considered. Recently [1] a general method for constructing nonGaussian stochastic processes has
been proposed, based on memoryless transformation of stationnary Gaussian processes.
Moreover the Gaussian process can be considered as a diffusion, solution of a stochastic differential equation.
Assuming that the diffusion has the good properties, this permits the use of Oseledets' results
for studying the stability of a dynamical system with non-Gaussian multiplicative noise.
The purpose of this paper is to highlight the incidence of the noise probability distribution on the stability
of an airfoil when the longitudinal turbulence component is introduced as a non-Gaussian noise.
In a first stage, the state space model is derived for the airfoil-aerodynamic coupled system.
Using rational approximation of the aerodynamic forces [5], the system motion equation can be
written:
where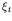 is a multiplicative noise wich can model for instance
longitudinal turbulence.
Using the method described in [1], the non-Gaussian process
is a multiplicative noise wich can model for instance
longitudinal turbulence.
Using the method described in [1], the non-Gaussian process 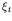 is constructed using
a truncated Hermite chaos polynomial expansion:
is constructed using
a truncated Hermite chaos polynomial expansion:
where
The Lyapounov exponent is finally constructed, using a simulated sample path of equation (93) solution:
In this paper our goal is to consider the effect of the distribution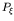 on the overall stability.
We will consider here two families of distribution,
the centered exponential distribution,
on the overall stability.
We will consider here two families of distribution,
the centered exponential distribution,
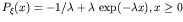 and the centered Rayleigh distribution,
and the centered Rayleigh distribution,
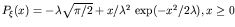 .
The spectrum
.
The spectrum 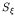 will be modeled by the von Karman model.
Numerical results show , as it was noticed in [2,4] for Gaussian noise,
that if multiplicative noise has an impact on the stability of the linear airfoil, so does the
distribution of the multiplicative noise, the more nonGaussian the distribution is the more
important the effect. In presence of freeplay, the role of the noise distribution
is crucial since, for this particular application, a Gaussian noise does not change significally
the stability behaviour of the airfoil.
will be modeled by the von Karman model.
Numerical results show , as it was noticed in [2,4] for Gaussian noise,
that if multiplicative noise has an impact on the stability of the linear airfoil, so does the
distribution of the multiplicative noise, the more nonGaussian the distribution is the more
important the effect. In presence of freeplay, the role of the noise distribution
is crucial since, for this particular application, a Gaussian noise does not change significally
the stability behaviour of the airfoil.
where
where
The Lyapounov exponent is finally constructed, using a simulated sample path of equation (93) solution:
In this paper our goal is to consider the effect of the distribution
References
- 1
- B. Puig, F.Poirion and C. Soize, "Non-Gaussian simulation using Hermite polynomial expansion: convergences and algorithms", Prob. Eng. Mech., Vol. 17, No. 3, 253-264, 2002. doi:10.1016/S0266-8920(02)00010-3
- 2
- I. Zentner and F. Poirion, "Stability of fluid-structure coupled systems in the presence of multiplicative and additive noise. Application to airfoil flutter", 7th ICCST proceedings , CDrom, 2004.
- 3
- L. Arnold, Random dynamical systems, Springer Verlag, Berlin Heidelberg 1998.
- 4
- D. Poirel and S. Price, "Response probability structure of a structurally non-linear airfoil in turbulent flow", Probabilistic Engineering Mechanics, Vol. 18, 2003.
- 5
- F. Poirion, "On some stochastic methods applied to aeroservoelasticity", Aerospace Science and Technology, No. 4, 2000, 201-214. doi:10.1016/S1270-9638(00)00118-8
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)
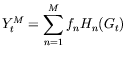
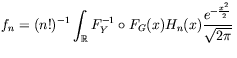 d
d