Keywords: potential theory, waves, current, inhomogeneous condition, semi-analytical formulation, Sturm-Liouville problem.
The scope of the present paper is the derivation of a semi-analytical formulation
for the first-order diffraction potential due to the presence of a vertical
surface-piercing cylinder in a flow field in which waves and currents coexist. The specific
subject is very important for offshore applications in which floating or fixed
structures usually consist of cylindrical elements. In addition the wave-current
interaction with a floating structure may be regarded as the opposite problem of the
structure moving with a slow speed in a wave field. Usually the methods
implemented for treating this problem are numerical [
1,
2]. This is due to the fact
that the presence of the current is accommodated in the free surface boundary
condition which in turn becomes inhomogeneous. The inhomogeneous form of the
associated equation makes the analytical approach of the solution more difficult for
the diffraction potential. On the other hand the derivation of a closed-form solution
for the scattered velocity potential due to the presence of a structure within the
wave-current flow field provides a robust and reliable tool for calculating the
induced hydrodynamic forces, the wave drift damping and the wave run-up on the
structural elements. In the present work this is performed by seeking a
semi-analytical formulation for the diffraction potential of the resulting complex flow
field.
As mentioned before, the main difficulty arises from the boundary condition on
the free surface for which it can be shown that it is given by the following relation.
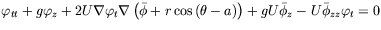 |
(91) |
where
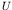
is the uniform current velocity,
r,
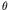
and
z are the coordinates of the
cylindrical coordinate system,
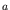
is the heading angle of the current,
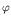
is the total
potential of the wave field and finally
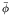
is the steady state potential that describes
the perturbation of the current due to the presence of the body. For treating the
resulting hydrodynamic problem a perturbation method is followed according to
which the diffraction potential that participates in the total potential
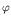
and is
influenced by the velocity of the current is analyzed in a perturbation series with
respect to the powers of the normalized velocity
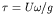
. Then the diffraction
potential is decomposed into a sufficient number of components which are used for
the proper satisfaction of all relevant boundary conditions. Thus, a Sturm-Liouville
problem is derived which is treated using the method of integral equations. The
solution of the associated problem requires the construction of a one-dimensional
Green's function and the manipulation of the inhomogeneous term in order to derive
the radial dependent effective pressure distribution on the free surface. Finally the
implementation of the above described derivation procedure results in the following
form for the current dependent diffraction component:
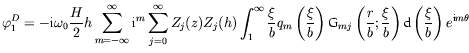 |
(92) |
where
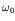
and
H/2 are the frequency and the amplitude of the undisturbed incident
wave,
h is the water depth,
qm is the radial dependent effective pressure distribution
on the free surface,
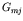
is the one dimensional Green's function and
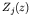
denotes the
vertical eigenfunctions.
The results presented in the paper depict the variation of the complex effective
pressure distribution for various eigenmodes. It is shown that although this term is
convergent for
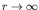 the integrand of the above equation does not reach a bound
limit. This is reflected also on the variation of the diffraction potential
the integrand of the above equation does not reach a bound
limit. This is reflected also on the variation of the diffraction potential
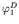 and
consequently for the total velocity potential of the combined wave-current field. This
remark that was highlighted by other authors in the past [3,4], is discussed in the
present work using the asymptotic forms of the Bessel functions.
and
consequently for the total velocity potential of the combined wave-current field. This
remark that was highlighted by other authors in the past [3,4], is discussed in the
present work using the asymptotic forms of the Bessel functions.
- 1
- B. Buchmann, J. Skourup and K.F. Cheung, K.F, "Run-up on a structure due to second-order waves and current in a numerical wave tank", Applied Ocean Research, 20, 297-308, 1998. doi:10.1016/S0141-1187(98)00022-4
- 2
- M.H. Kim, M.S. Celebi and D.J. Kim, "Fully nonlinear interactions of waves with a three-dimensional body in uniform currents", Applied Ocean Research, 20, 309-321, 1998. doi:10.1016/S0141-1187(98)00025-X
- 3
- G. Bannister, "Wave/current forces on axisymmetrical bodies with vertical axes", Ship Technology Research, 40, 138-156, 1993.
- 4
- S. Malenica, P.J. Clark and B. Molin, "Wave and current forces on a vertical cylinder free to surge and sway", Applied Ocean Research, 17, 79-90, 1995. doi:10.1016/0141-1187(95)00002-I
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)

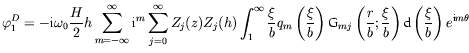
![]() the integrand of the above equation does not reach a bound
limit. This is reflected also on the variation of the diffraction potential
the integrand of the above equation does not reach a bound
limit. This is reflected also on the variation of the diffraction potential
![]() and
consequently for the total velocity potential of the combined wave-current field. This
remark that was highlighted by other authors in the past [3,4], is discussed in the
present work using the asymptotic forms of the Bessel functions.
and
consequently for the total velocity potential of the combined wave-current field. This
remark that was highlighted by other authors in the past [3,4], is discussed in the
present work using the asymptotic forms of the Bessel functions.