Keywords: reinforced earth, discrete element method, numerical analysis, slope stability, ground improvement, soil reinforcement.

Reinforced earth is the name of a patented system to stabilize soil slopes, which originated in 1966 by Vidal [1]. There are some analytical methods to analyze reinforced earth such as the "Coulomb force method" [2]. But most of them are not capable of finding each reinforcement force. They can only calculate the total force of the reinforcement elements. In this study, a new procedure using the discrete element method, (DEM), is presented for the stability analysis of reinforced earth. Change [3] proposed the first technique of discrete element method, to solve a non-reinforced slope. In this method a whole slope is replaced by discrete slices, which are connected with elasto-plastic Winkler springs. Definition of the spring's behavior is based on the Mohr-Coulomb criterion. Normal springs do not yield in compression, but they yield in tension. The shear springs yield when the final soil shear strength is reached according to the Mohr-Coulomb criterion. In this research, the effect of reinforcement is considered as a normal and a shear spring acted on the intersection between the reinforcement and the potential failure surface. The reinforcement shear, is calculated by using the equation of elastic bending and by assuming that the soil can be replaced by a series of elasto-plastic springs. As a result, , is obtained for the stiffness of shear springs in the reinforcement elements. ( = bending stiffness of reinforcement, , modulus of soil reaction, and b = reinforcement width). The normal spring stiffness of reinforcement is calculated by modification of the formulation of Mitachi et al. [4] formulation:

Where u = relative displacement between the soil and the reinforcement element, x = the distance from the in-soil end of reinforcement, the stiffness of tensile force vs. strain relationship of reinforcement, and and are the residual shear strength and relative displacement corresponding to , respectively. Solving these equations by applying boundary conditions, results in a normal stiffness of the reinforcement at the intersection between reinforcement and failure surface.

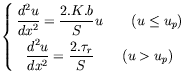
The final stiffness matrix is obtained by a combination of soil and reinforcement stiffness. Then the program employs different shapes of failure surfaces. By applying the external load to each potential failure surface, displacements and forces can be obtained by a non-linear procedure. In each step there are some springs and have yielded their stiffness should be decreased. The convergence control is satisfied by minimizing the difference between the resultant of the external forces, and the resultant of the internal forces. Finally the failure surface is the one that represents the maximum forces of the reinforcement. In contrast with other conventional limit equilibrium methods, the discrete element is capable of calculating the distribution of forces in the reinforcement and presenting local safety factors at each soil and reinforcement element. The results of examples presented in the full text paper, have shown a good correspondence between the discrete element analysis and the experimental results [5]. Also another feature of the discrete element method, is that, while others approaches have several difficulties in the analysis of stratification and complicated geometries, the DEM can easily consider these cases in its modeling.

1

H. Vidal, "Reinforced Earth (French)" Annales Inst. Tech. du Batiment et des Travaux Publiques, France, Nos.228-229, pp. 888-938,1966.

2

F. Schlosser, H. Vidal "La terre armée", Bull. de Liais. LCPC, No. 41, (November), pp.101-144,1969.

3

C.S. Chang, "A Discrete Element Method for Slope Stability Analysis", Journal of Geotechnical Engineering, ASCE, Vol.118, No.12, pp.1889-1906,1992. doi:10.1061/(ASCE)0733-9410(1992)118:12(1889)

4

T. Mitachi, Y. Yamamoto, S. Muraki, "Estimation of In-Soil Deformation Behavior of Geogrid Under Pull-out Loading", Proceeding of the International Symposium on Earth Reinforcement Practice, Japan, Vol.1, pp.121-126,1992.

5

F. Schlosser, "Mechanically Stabilized Earth Retaining Structure in Europe", Proc. ASCE Conf. on Design and Performance of Earth Retaining Structures, Ithaca, N.Y., pp.347-378,1990.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)