Keywords: intelligent system, formal ontology, structural engineering, long tunnels, upgrade procedures.

The representation of the geometry of structures is a fundamental issue in several engineering computer applications. The geometry of tunnels present a variety of different problems that have been solved in many different ways depending upon the context in which they have been formulated, the general approach that has been adopted for the application and the target users of the application itself.

In this paper we provide a family of solutions to the problem of representing the geometry of tunnels in an application whose purpose is the assistance to a team that operates the tunnel upgrade to functional and prescriptive requirements. The paper addresses the problem in three different steps:

1. We formulate the problem in a general framework, associated with the question of defining the basic constraints that the geometry of a tunnel should respect; in this phase we pose specific attention to the solution strategy, and in particular to the solution methodology;
2. We embed the general framework into the specific application and analyze the several levels at which the geometric analysis can be performed;
3. We provide a formalization of the proposed models into a logical theory, the description logic 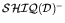that has been employed in various cases of engineering, in particular in the context of civil and structural engineering.

There are fundamentally five different directions in which the geometry of a tunnel can be specified and we provide the full combinatorial analysis of the deployments of these models in based upon the implementation of different rewriting operators. The paper concentrates upon the five directions, the combinatorial explosion analysis, the analysis of the resulting formalizations, in terms of correctness, completeness and the complexity of reasoning.

The five directions in which the geometry of tunnels can be formalized are:

1. The dimensions in which the tunnel is represented. We can have one-dimensional formalisations in two-dimensional space, or one-dimensional in three-dimensional, or we can have two-dimensional representations in two or three dimensions, and finally full three-dimensional representations;
2. The structure of the part or whole relationships among pieces of tunnels and complete tunnels, in particular the notion of "gallery", a part of a tunnel that, trivially, cannot be a tunnel itself; this is named the mereology of tunnels;
3. The properties attached to the tunnels, or to the parts of the tunnel; in particular the physical properties, parameters of the tunnel itself, like the performance of concrete at high temperature, the maximum load of asphalt and many others;
4. The shape of the tunnel entrances, described in both abstract "nominal shape" or concrete "Jordan curve types";
5. The geographic location of the tunnel, in particular the GPS coordinates associated to the parts of the tunnel, and the height quotes relative to the sea level.

The paper also proves that a general methodology can be formed based upon the substitution of the terms that are specific to tunnels with generic terms referring to structures.

purchase the full-text of this paper (price £20)

go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)