engineering & technology publications
ISSN 1759-3433
PROCEEDINGS OF THE FIFTH INTERNATIONAL CONFERENCE ON ENGINEERING COMPUTATIONAL TECHNOLOGY
An Artificial Immune System Algorithm for Structural Optimization
Department of Mechanical and Electro-Mechanical Engineering, Tamkang University, Tamsui, Taiwan R.O.C.
Learning, memory, diversity, hyper-mutation, differentiation and natural selection are the primary operators to ensure the proposed approach has the global as well as the local search potential. The technique of hyper-mutation is extensively modified to fulfil the primary search that shows effectively powerful. Numerically, one can replicate the adaptive immune system to proliferate diversity immune cells for bind pathogens. An algorithm of simulating the affinity maturation is as follows:
- Recognize the pathogens.
- Start to activate the memory cells of lymphocytes (called B-cells) and produce the required diversity with a pseudo-random process.
- B-cell cloning is subject to a somatic hyper-mutation.
- The new B-cell clones succeed to bind pathogenic, they will differentiate into plasma B-cells or memory B-cells. Plasma B-cells secrete a soluble form of their receptors, called antibodies.
- Repeat the cycle of affinity maturation (step 2 to 4) until high-affinity B-cells are obtained.
For example, a 72-bar space truss is required to support two load conditions given
in reference [2] and is to be designed with allowable constraints and the allowable
displacements. This problem was solved by the proposed approach in which the
total population is 100, the maximum generations ![]() is 300. Other prescribed
number of group population are
is 300. Other prescribed
number of group population are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Using the
proposed immune based approach to solve the problem ten times to find the
optimum cross-sectional area of 16 members by minimizing the total structural
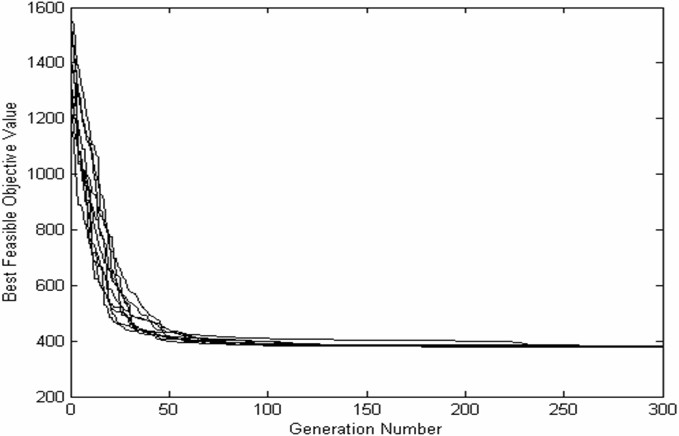
weight. Figure 1 shows the iteration history of the ten searches for the optimum. It
is obvious to see that the proposed method is robust and gives accurate results.
. Using the
proposed immune based approach to solve the problem ten times to find the
optimum cross-sectional area of 16 members by minimizing the total structural
weight. Figure 1 shows the iteration history of the ten searches for the optimum. It
is obvious to see that the proposed method is robust and gives accurate results.
- 1
- Hofmeyr, S.A., An Interpretative Introduction to the Immune System, Design principles for the Immune System and Other Distributed Autonomous Systems, Eds. Ohen, I. and Segel, L., Oxford University Press, 2000.
- 2
- Haftka, R. T. and Gurdal, Z., Elements of structural optimization, Kluwer Academic publishers, pp. 245-248, 1992.
purchase the full-text of this paper (price £20)
go to the previous paper
go to the next paper
return to the table of contents
return to the book description
purchase this book (price £105 +P&P)